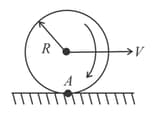
A point is located on the rim of a wheel of radius which rolls without slipping along a horizontal surface with velocity as shown in figure. Find:
(a) the modulus and the direction of the acceleration vector of the point ;
(b) the total distance s traversed by the point between the two successive moments at which it touches the surface.


Important Questions on Rotational Mechanics
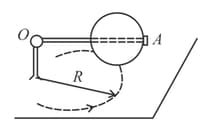
A uniform sphere of mass and radius rolls without sliding over a horizontal plane, rotating about a horizontal axle . In the process, the centre of the sphere moves with velocity along a circle of radius Find the kinetic energy of the sphere.
Consider a bicycle in vertical position accelerating forward without slipping on a straight horizontal road. The combined mass of the bicycle and the rider is and the magnitude of the accelerating torque applied on the rear wheel by the pedal and gear system is . The radius and the moment of inertia of each wheel is and (with respect to the axis) respectively. The acceleration due to gravity is .
(a) Draw the free diagram of the system (bicycle and rider ).
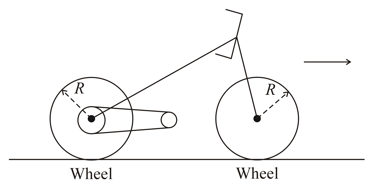
(b) Obtains the acceleration in terms of the above-mentioned quantities.
(c) For simplicity assume that the centre of mass of the system is at height from the ground and equidistant at from the centre of each of the wheels. Let be the coefficient of friction (both static and dynamic) between the wheels and the ground. Consider and no slipping. Obtain the conditions for the maximum acceleration of the bike.
(d) For calculate .
