A point-charge is placed at the centre of a closed Gaussian spherical surface. How is electric flux , through the surface affected when
The sphere is replaced by a cylinder of the different volume?

Important Questions on Gauss' Theorem
A point-charge is placed at the centre of a closed Gaussian spherical surface. How is electric flux , through the surface affected when
(ii) The charge is shifted from the centre to some other place inside the sphere?
A point-charge is placed at the centre of a closed Gaussian spherical surface. How is electric flux , through the surface affected when
(iii) A second charge is placed inside the sphere?
A point-charge is placed at the centre of a closed Gaussian spherical surface. How is electric flux , through the surface affected when
(iv) The charge is replaced by an electric dipole?
Suppose a Gaussian surface does not have any net charge inside it. Does it mean that the electric intensity is necessarily zero at all points on the surface? Is the converse true?
A cylindrical Gaussian surface has its axis along an infinite line of uniformly distributed positive charges, as shown.
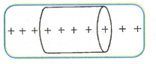
(i) For which surface is the electric flux zero?
A cylindrical Gaussian surface has its axis along an infinite line of uniformly distributed positive charges, as shown.
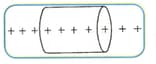
Over which surface is zero?
