A point charge is at the origin. It has velocity . Find the magnetic field at the following points in vector form (at the moment when the charged particle passes through the origin):
(i)
(ii)
(iii)
(iv)
(v) Is the magnitude of the magnetic field on the circumference of the circle (in plane) , where is a constant is same everywhere. Is it same in direction also?
(vi) Answer the above (v) for the circle of same equation but in a plane , where is a constant.

Important Questions on Magnetic Effect of Current
A particle of negative charge of magnitude is revolving with constant speed in a circle of radius as shown in the figure. Find the magnetic field (magnitude and direction) at the following points:
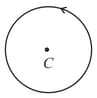
(i) centre of the circle (magnitude and direction)
(ii) a point on the axis and at a distance from the centre of the ring (magnitude only). Is its direction constant all the time?
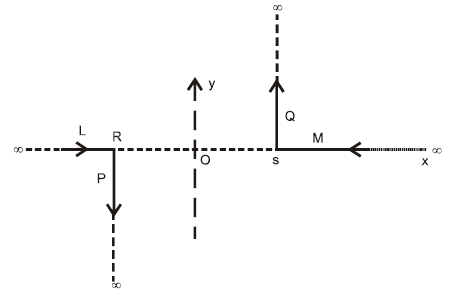
A pair of stationary and infinitely long bent wires is placed in the plane as shown in the figure. The wires carry currents of each as shown. The segments and are along the -axis. The segments and are parallel to the -axis such that . Find the magnitude and direction of the magnetic induction at the origin .
Two straight infinitely long and thin parallel wires are spaced apart and carry a current of each. Find the magnetic field at a point distant from both wires in the two cases when the currents are in the
(i) Same and
(ii) Opposite direction.
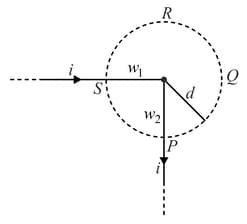
The figure shows a long wire bent in the middle to form a right angle. Show that the magnitudes of the magnetic fields at the points and are unequal and find these magnitudes. The wire and the circumference of a circle are coplanar and is perpendicular to the plane of the paper. Also, find the ratio of the field at and ,
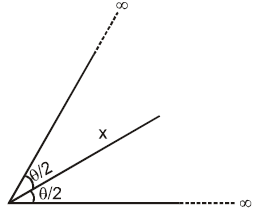
A long wire carrying a current is bent to form a plane angle . Find the magnetic field at a point on the bisector of this angle situated at a distance from the vertex is written in the form of . Then, find the value of .
(i) Two circular coils of radii and carry equal currents of . The coils have and turns respectively and are placed in such a way that their planes, as well as the centre, coincide. Find the magnitude of the magnetic field at the common center when the currents in the coils are (a) in the same sense (b) in the opposite sense. (ii) If the outer coil of the above problem is rotated through about a diameter, what would be the magnitude of the magnetic field at the centre?
