A point moves with deceleration along the circle of radius so that at any moment of time, its tangential and normal accelerations are equal in moduli. At the initial moment , the velocity of the point equals . Find,
the velocity of the point as a function of time and as a function of the distance covered .
the total acceleration of the point as a function of velocity and the distance covered.
the velocity of the point as a function of time and as a function of the distance covered .
the total acceleration of the point as a function of velocity and the distance covered.

Important Questions on PHYSICAL FUNDAMENTALS OF MECHANICS
the magnitude of the total acceleration of the particle at the points and
the minimum value of the total acceleration and the corresponding displacement .
of a parabola ,
of an ellipse and are constants here.
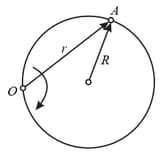
A particle moves along a circle of radius , so that its radius vector relative to the point rotates with the constant angular velocity . Find the modulus of velocity of the particle, and the modulus and direction of its total acceleration.
A solid body rotates about a stationary axis according to the law, , where and . Find:
(a) the mean values of the angular velocity and angular acceleration, averaged over the time interval between and then complete stop;
(b) the angular acceleration at the moment when the body stops.
