HARD
CAT
IMPORTANT
Earn 100

A rectangular box of volume 48 cu.ft is to be constructed, so that its length is twice its width. The material to be used for the top and the four sides is three times costlier per ft2 than that used for the bottom. Then, the height (in ft) of the box that minimizes the cost is equal to:

50% studentsanswered this correctly

Important Questions on X+2 Maths

EASY
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 3 - X+2 Maths>Practice Exercises>Q 39
A truck is to be driven for 300 km on a highway at a constant speed of x km/h. The speed rules of the highway require 30≤x≤60. The fuel costs ₹ 10 per litre and is consumed at the rate of 2+x2600 liters per hour. The wages of the driver are ₹ 200 per hour. The most economical speed to drive the truck, in km/h, is:
HARD
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 3 - X+2 Maths>Practice Exercises>Q 41
How many integral points are there within the graph of |x|+|y|≤4?
HARD
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 3 - X+2 Maths>Practice Exercises>Q 42
The sides of a rectangle of the greatest area that can be inscribed into an ellipse x225+y29=1 is:
HARD
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 3 - X+2 Maths>Practice Exercises>Q 43
The sets

{[x,y]:|y-1|-x≥1}

{[x,y]:|x|-y≥1}

{[x,y]:|x-1|+y≥0}

{[x,y]:y-|x-1∣≥0}

are represented by the shaded regions in the figures given below in some order.

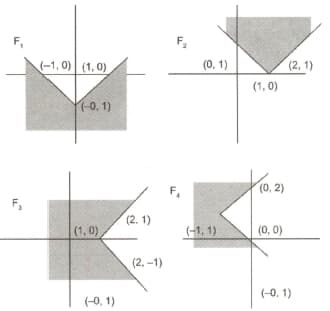
Question Image 

The correct order of the figures is:
HARD
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 3 - X+2 Maths>Practice Exercises>Q 47
From a square tin sheet of side 12 feet, a box with its top open is made by cutting equal squares at the four corners and then bending the tin sheet so as to form the sides of the box. The side of the removed square for which the box has the maximum possible volume in feet is:
HARD
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 3 - X+2 Maths>Practice Exercises>Q 48
From a circular sheet of paper of radius a, a sector with a central angle is cut out and folded into the shape of a conical funnel. The volume of this funnel is maximum when θ equals:
MEDIUM
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 3 - X+2 Maths>Practice Exercises>Q 1

Find the equation of the graph shown below.

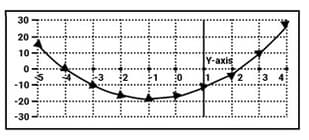
Question Image

MEDIUM
CAT
IMPORTANT
Quantitative Aptitude for the CAT>Chapter 3 - Measurement>Practice Exercises>Q 5
A square tin sheet of side 12 inches is converted into a box with open top in the following steps. The sheet is placed horizontally. Then, equal-sized squares, each of side x inches, are cut from the four corners of the sheet. Finally, the four resulting sides are bent vertically upwards in the shape of a box. If x is an integer, then what value of x maximizes the volume of the box?