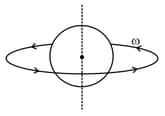
A ring of mass $m$ and radius $3R$ is rotating with constant angular speed $\omega \left(\omega =\sqrt{\frac{GM}{9R^3}}\right)$ around a planet of mass $M$ and radius $R$. Center of ring and planet coincide with each other. Tension in the ring is given as $T=\frac{GMm}{3n\pi R^2}$. Find value of $n$. (Assume elements of the ring don't gravitationally interact with each other)

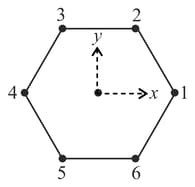
Six objects are placed at the vertices of $\mathrm{a}$ regular hexagon. The geometric centre of the hexagon is at the origin with objects $1$ and $4$ on the $X$-axis (see figure). The mass of the $\mathrm{k}$ th object is ${\mathrm{m}}_{\mathrm{k}}={\mathrm{k}}^{\mathrm{i}}\mathrm{M}\left|{\mathrm{cos\theta }}_{\mathrm{k}}\right|,$ where $\mathrm{i}$ is an integer, $\mathrm{M}$ is $\mathrm{a}$ constant with dimension of mass and ${\mathrm{\theta }}_{\mathrm{k}}$ is the angular position of the $\mathrm{k}$ th vertex measured from the positive $\mathrm{x}$ -axis in the counter-clockwise sense. If the net gravitational force on $\mathrm{a}$ body at the centroid vanishes, the value of $\mathrm{i}$ is

Four identical particles of mass $\mathrm{M}$ are located at the corners of a square of side $‘a’$ . What should be their speed if each of them revolves under the influence of other’s gravitational field in a circular orbit circumscribing the square?