A rod of length $2 \mathrm{m}$ rests on a smooth horizontal floor. If the rod is heated from $0°\mathrm{C} \text{to} 20°\mathrm{C}$, find the longitudinal strain developed ($\alpha =5\times {10}^{-5} °{\mathrm{C}}^{-1}$).

Two wires are made of the same material and have the same volume. The first wire has cross-sectional area $A$ and the second wire has cross-sectional area $3A$. If the length of the first wire is increased by $\Delta l$ on applying a force $F$ how much force is needed to stretch the second wire by the same amount?

A string is stretched between two fixed points separated by $75 \mathrm{cm}.$ It is observed to have resonant frequencies of $420 \mathrm{Hz} \mathrm{and} 315 \mathrm{Hz}.$ There are no other resonant frequencies between these two. Then, the lowest resonant frequency for this string is :

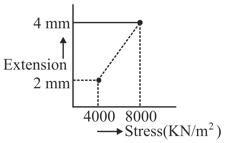
In determining Young’s modulus of elasticity of wire, a force is applied and extension is recorded. Initial length of wire is $1 \mathrm{m}$. The curve between extension and stress is depicted. Then, Young’s modulus of wire will be,