A rotating disc (figure) moves in the positive direction of the -axis. Find the equation describing the position of the instantaneous axis of rotation, if at the initial moment the axis of the disc was located at the point after which it moved.
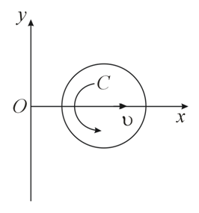
(a) With a constant velocity , while the disc started rotating counter clockwise with a constant angular acceleration (the initial angular velocity is equal to zero);
(b) With a constant acceleration a (and the zero initial velocity), while the disc rotates counterclockwise with a constant angular velocity .


Important Questions on Rotational Mechanics
A block of mass is held by a long massless string on a fixed frictionless inclined plane inclined at to the horizontal. The string is wound on a uniform solid cylindrical drum of mass and radius as shown in the figure. The drum is given an initial angular velocity such that block starts moving up the plane.
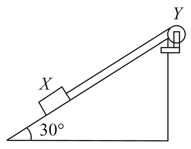
(a) Find the tension in the string during motion.
(b) At a certain instant of time, the magnitude of the angular velocity of is . Calculate the distance travelled by from that instant of time until it comes to rest.
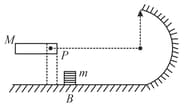
A rod of length and mass is free to rotate about a horizontal axis passing through hinge as in the figure. First it is taken aside such that it becomes horizontal and then released. At the lowest point, the rod hits the small block of mass and stops. Find the ratio of masses such that the block completes the circular track of radius . Neglect any friction.
A plank of mass , with a uniform sphere of mass placed on it, rests on a smooth horizontal plane. A constant horizontal force is applied to the plank. With what accelerations will the plank and the centre of the sphere move, provide there is no sliding between the plank and the sphere?
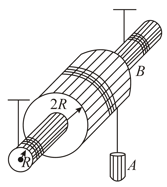
In the arrangement shown in the figure, weight possesses mass , a pulley possesses mass . Also known are the moment of inertia of the pulley relative to its axis and the radii of the pulley are and , respectively. Consider the mass of the threads is negligible. Find the acceleration of weight after the system is set free. (Assume no slipping takes place anywhere and axis of cylinder remains horizontal)
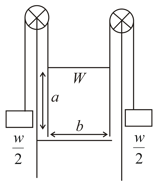
A window (of weight ) is supported by two strings passing over two smooth pulleys in the frame of the window in which window just fits in, the other ends of the string being attached to weights each equal to half the weight of the window. One thread breaks and the window moves down. Find acceleration of the window if is the coefficient of friction, and is the height and the breadth of the window.
A diameter pipe of mass rests on a plate. The pipe and plate are initially at rest when a force of magnitude is applied for . Knowing that between the plate and both the pipe and the floor, determine;
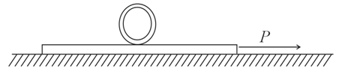
(a) whether the pipe slides with respect to the plate.
(b) the resulting velocities of the pipe and of the plate.
