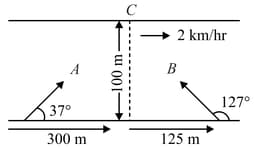
A ship is moving at a constant speed of $10\mathrm{kmhr}$ in the direction of the unit vector $\hat{i}$. Initially, its position vector, relative to a fixed origin is $10\left(-\hat{i}+\hat{j}\right)$ where $\hat{i} \& \hat{j}$ are perpendicular vectors of length $1\mathrm{km}$. Find its position vector relative to the origin at time $t$ hours later. A second ship is moving with constant speed $u {\mathrm{kmhr}}^{-1}$ parallel to the vector $\hat{i}+2\hat{j}$ and is initially at the origin.

(i) If $u=10\sqrt{5} {\mathrm{kmh}}^{-1}$. Find the minimum distance between the ships and the corresponding value of $t$

(ii) Find the value of $u$ for which the ships are on a collision course and determine the value of $t$ at which the collision would occur if no avoiding action were taken.

A balloon starts ascending from the ground at a constant speed of $25{\mathrm{ms}}^{-1}$. After $5\mathrm{s}$, a bullet is shot vertically upward from the ground.

(i) What should be the minimum speed of the bullet so that it may reach the balloon?

(ii) The bullet is shot at twice the speed calculated in (i). Find the height at which it passes the balloon.

Two swimmers start a race. One who reaches the point $C$ first on the other bank wins the race. A makes his strokes in a direction of $37°$ to the river flow with velocity $5{\mathrm{kmhr}}^{-1}$ relative to water. $B$ makes his strokes in a direction $127°$ to the river flow with same relative velocity. River is flowing with speed of $2 {\mathrm{kmhr}}^{-1}$ and is $100\mathrm{m}$ wide. Who will win the race? Compute the time taken by $A$ and $B$ to reach the point $C$ if the speed of $A$ and $B$ on the ground are $8 {\mathrm{kmhr}}^{-1}$ and $6 {\mathrm{kmhr}}^{-1}$ respectively.

A swimmer starts to swim from point $A$ to cross a river. He wants to reach point $B$ on the opposite side of the river. The line $AB$ makes an angle $60°$ with the river flow as shown. The velocity of the swimmer in still water is same as that of the water

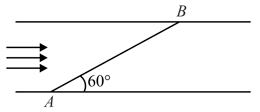
 (i) In what direction should he try to direct his velocity? Calculate angle between his velocity and river velocity.

(ii) Find the ratio of the time taken to cross the river in this situation to the minimum time in which he can cross this river.

Two inclined planes $OA$ and $OB$ having inclinations $30°$ and $60°$ respectively, intersect each other at $O$ as in figure. A particle is projected from point $P$ with velocity $u=10\sqrt{3} {\mathrm{ms}}^{-1}$ along a direction perpendicular to plane $OA$. If the particle strikes the plane $OB$ perpendicularly at $Q$. Calculate

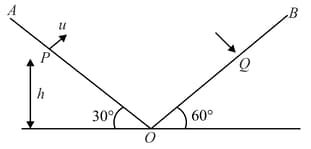
(i) Time of flight.

(ii) Velocity with which particle strikes the plane $OB$.

(iii) Vertical height of $P$ from $O$

(iv) Maximum height from $O$ attained by the particle.

(v) Distance $PQ$.