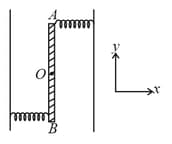
A simple pendulum and a homogeneous rod pivoted at its end are free to oscillate with small amplitude. What is the ratio of their periods of swing if their lengths are identical?

 

The position co-ordinates of a particle moving in a $3D$ coordinate system is given by

$x=a\cos \mathrm{\omega }\mathrm{t}$

$y=a\sin \omega t$

and $z=a\omega t$

The speed of the particle is:

An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass $\mathit{\text{M}}$. The piston and the cylinder have equal cross-sectional area $\mathit{\text{A}}$. When the piston is in equilibrium, the volume of the gas is $V_0$ and its pressure is $M_0$. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surrounding, the piston executes a simple harmonic motion with frequency
[Assume the system is in space.]

A particle of mass $1 \mathrm{mg}$ and charge $q$ is lying at the mid-point of two stationary particles kept at a distance $2 \mathrm{m}$ when each is carrying same charge $q$. If the free charged particle is displaced from its equilibrium position through distance $x$ $\left(x<<1 \mathrm{m}\right)$. The particle executes SHM. Its angular frequency of oscillation will be _______ $\times {10}^5 \mathrm{rad} {\mathrm{s}}^{-1}$ (if $q^2=10C^2$)

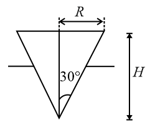
A cone with half the density of water is floating in water as shown in figure. It is depressed down by a small distance $\delta \left(\ll \mathrm{H}\right)$ and released. The frequency of simple harmonic oscillations of the cone is

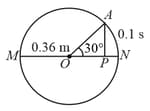
The point $A$ moves with a uniform speed along the circumference of a circle of radius $0.36 \mathrm{m}$ and covers $30°$ in $0.1 \mathrm{s}$. The perpendicular projection $P$ from $A$ on the diameter $MN$ represents the simple harmonic motion of $P$. The restoration force per unit mass when $P$ touches $M$ will be :