A simple pendulum has time-period $T_1$. The point of suspension is now moved upward according to the relation $y=k{t}^2$, $\left(k=1{\mathrm{ms}}^{-2}\right)$ where $y$ is the vertical displacement. The time period now becomes $T_2$. The ratio of $\frac{{\mathrm{T}}_1^2}{{\mathrm{T}}_2^2}$ is ($g=10 {\mathrm{ms}}^{-2}$)

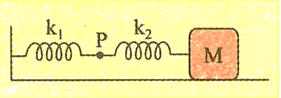
Two masses $m_1$ and $m_2$ are suspended together by a massless spring of constant $k$. When the masses are in equilibrium, $m_1$ is removed without disturbing the system. The amplitude of oscillation is

A uniform rod of length $L$ and mass $M$ is pivoted at the centre. Its two ends are attached to two springs of equal spring constants $k$. The springs are fixed to the rigid supports as shown in Fig 22.70, and rod is free to oscillate in the horizontal plane. The rod is gently pushed through a small angle $\theta$ in one direction and released. The frequency of oscillation is

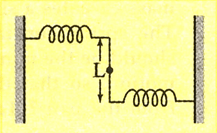
The mass $M$ shown in Fig 22.71 oscillates in simple harmonic motion with amplitude $A$. The amplitude of the point $P$ is

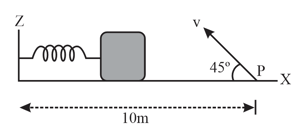
A small block is connected to one end of a massless spring of unstretched length $4.9 \mathrm{m}$. The other end of the spring is fixed. The system lies on a horizontal frictionless surface. The block is stretched by $0.2 \mathrm{m}$ and released from rest at $t=0$. It then executes simple harmonic motion with angular frequency $\omega =\frac{\pi }{3} \mathrm{rad} {\mathrm{s}}^{-1}$. Simultaneously at $t=0$, a small pebble is projected with speed $v$ from point $P$ at an angle of $45°$ as shown in the figure. Point $P$ is at a distance of $10 \mathrm{m}$ from $O$. If the pebble hits the block at $t=1 \mathrm{s}$, the value of $v$ is $\left(g=10 \mathrm{m} {\mathrm{s}}^{-2}\right)$

The amplitude of a damped oscillator decreases to $0.9$ times its original magnitude is $5 \mathrm{s}$. In another $10 \mathrm{s}$ it will decrease to $\alpha$ times its original magnitude, where $\alpha$ equals

An ideal gas enclosed in a vertical cylindrical container supports a freely moving piston of mass $M$. The piston and the cylinder have equal cross-sectional area $A$. When the piston is in equilibrium, the volume of the gas is $V_0$ and its pressure is $p_0$. The piston is slightly displaced from the equilibrium position and released. Assuming that the system is completely isolated from its surroundings, the piston executes a simple harmonic motion with the frequency