A particle is moving in x y plane. Its velocity and acceleration at a certain instant is given by v → = 3 i ^ + 4 j ^ m s - 1 and a → = 5 i ^ + 15 4 j ^ m s - 2 . Find the rate of change of speed (in m s - 2 ) of particle at that instant.

Given, velocity v → = 3 i ^ + 4 j ^ m s - 1 and acceleration a → = 5 i ^ + 15 4 j ^ m s - 1 ∴ x component of velocity, v x = 3 m s - 1 d component of velocity, v y = 4 m s - 1 , x component of acceleration, a y = 5 m s - 2 , d component of acceleration, a y = 15 4 m s - 2 As speed is the magnitude of velocity, so, speed is given by v = v x 2 + v d 2 = 3 2 + 4 2 = 5 m s - 1 Clearly, instantaneous speed v is given by v 2 = v x 2 + v d 2 Differentiating both sides respect to time t , we get, 2 v d v d t = 2 v x d v x d t + 2 v y d v y d t … 1 ∵ d v x d t = a x and d v y d t = a y ∴ Using 1 , we get, v d v d t = v x a x + v y a y ⇒ d v d t = 1 v v x a x + v y a y Putting values, we get, ⇒ d v d t = 1 5 3 × 5 + 4 × 15 4 ⇒ d v d t = 6 m s - 2 ∴ Rate of charge of speed is 6 m s - 2 .

A bob of mass 100 g is connected to a thread of length l and projected horizontally with speed of 6 g l so that it completes vertical circle. What is the difference between maximum tension and minimum tension (in N )?

Tension is maximum at the bottom and minimum at top. Let the tensions at bottom and top be T 1 and T 2 , respectively and speeds be v 1 and v 2 , respectively. Let the radius be R . Using Newton's 2 nd law at bottom, we get, T 1 - m g = m v 1 2 R … 1 . Using Newton's 2 nd law at top, we get, m g + T 2 = m v 2 2 R … 2 . Subtracting equation 2 from 1 , we get, T 1 - T 2 - 2 m g = m R v 1 2 - v 2 2 … 3 . Applying conservation of mechanical energy, we get, Loss in KE = gain in gravitational PE ⇒ 1 2 m v 1 2 - 1 2 m v 2 2 = m g 2 R ⇒ v 1 2 - v 2 2 = 4 g R … 4 . Putting 4 into 3 , we get, T 1 - T 2 - 2 m g = m R · 4 g R ⇒ T 1 - T 2 = 6 m g … 5

For a particle in uniform circular motion, the acceleration a → at a point P ( R , θ ) on the circle of radius R is (here, θ is measured from the x -axis),

- v 2 R sin θ i ^ + v 2 R cos θ j ^

- v 2 R cos θ i ^ + v 2 R sin θ j ^

- v 2 R cos θ i ^ - v 2 R sin θ j ^

HARD

JEE Advanced

IMPORTANT

Earn 100

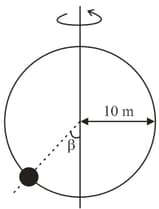
A small bead can slide without friction on a circular hoop that is in a vertical plane and has a radius of $10 m$ . The hoop rotates at a constant rate about a vertical diameter. Find the height of the bead (in $m$ ) above the bottommost point if the angular velocity of rotation is $0.5 rad s^{- 1}$ .

50% studentsanswered this correctly

Important Questions on Circular Motion

HARD

JEE Advanced

IMPORTANT

PHYSICS For Joint Entrance Examination JEE (Advanced) Mechanics I>Chapter 9 - Circular Motion>Exercises>Q 8

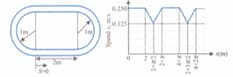
A toy car is moving anticlockwise on a closed track whose curved portions are semicircles of radius $1 m$ . The adjacent graph describes the variation of speed of the car with distance moved by it (starting from point $S$ ). Find the time $(t)$ required for the car to complete one lap in second, (take $π \ln (2) \approx 2$ )

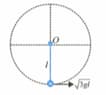
Question Image

HARD

JEE Advanced

IMPORTANT

PHYSICS For Joint Entrance Examination JEE (Advanced) Mechanics I>Chapter 9 - Circular Motion>Exercises>Q 9

Small parts each of mass $m$ on a conveyer belt moving with constant velocity are allowed to drop into a bin. Radius of circular portion is $2 m$ . The static coefficient of friction between the parts and belt $μ_{s}$ is $1$ . If the parts start sliding on the belt at the angle $α = 37^{o}$ . Find the velocity (in ${ms}^{- 1}$ ) of conveyer belt.

HARD

JEE Advanced

IMPORTANT

PHYSICS For Joint Entrance Examination JEE (Advanced) Mechanics I>Chapter 9 - Circular Motion>Exercises>Q 10

One end of a massless spring of spring constant

100 {Nm}^{- 1}

and natural length

0.5 m

is fixed and the other end is connected to a particle of mass

0.5 kg

lying on a frictionless horizontal table. The spring remains horizontal. If the mass is made to rotate at an angular velocity of

2 {rads}^{- 1}

, find the elongation of the spring (in

cm

MEDIUM

JEE Advanced

IMPORTANT

PHYSICS For Joint Entrance Examination JEE (Advanced) Mechanics I>Chapter 9 - Circular Motion>Exercises>Q 11

A particle is moving in

x y

plane. Its velocity and acceleration at a certain instant is given by

\vec{v} = (3 \hat{i} + 4 \hat{j}) m s^{- 1}

and

\vec{a} = (5 \hat{i} + \frac{15}{4} \hat{j}) m s^{- 2}

. Find the rate of change of speed (in

m s^{- 2}

) of particle at that instant.

HARD

JEE Advanced

IMPORTANT

PHYSICS For Joint Entrance Examination JEE (Advanced) Mechanics I>Chapter 9 - Circular Motion>Exercises>Q 12

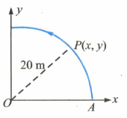
A ball is given a velocity of $\sqrt{3 g l}$ as shown. If the ratio of centripetal acceleration to tangential acceleration is $1 : y \sqrt{2}$ at the point where the ball leaves circular path then write the value of $y$ . [Neglect the size of ball]

Question Image

HARD

JEE Advanced

IMPORTANT

PHYSICS For Joint Entrance Examination JEE (Advanced) Mechanics I>Chapter 9 - Circular Motion>Exercises>Q 13

A bob of mass $100 g$ is connected to a thread of length $l$ and projected horizontally with speed of $\sqrt{6 g l}$ so that it completes vertical circle. What is the difference between maximum tension and minimum tension (in $N$ )?

Question Image

EASY

JEE Advanced

IMPORTANT

PHYSICS For Joint Entrance Examination JEE (Advanced) Mechanics I>Chapter 9 - Circular Motion>Archives>Q 1

For a particle in uniform circular motion, the acceleration $\vec{a}$ at a point $P (R, θ)$ on the circle of radius $R$ is (here, $θ$ is measured from the $x$ -axis),

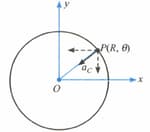
Question Image

EASY

JEE Advanced

IMPORTANT

PHYSICS For Joint Entrance Examination JEE (Advanced) Mechanics I>Chapter 9 - Circular Motion>Archives>Q 2

A point $P$ moves in counter-clockwise direction on a circular path as shown in the figure. The movement of $P$ is such that it sweeps out a length $s = t^{3} + 5$ , where $s$ is in metres and $t$ is in seconds. The radius of the path is $20 m$ . The acceleration of $P$ when $t = 2 s$ is nearly,

Question Image

A small bead can slide without friction on a circular hoop that is in a vertical plane and has a radius of 10 m. The hoop rotates at a constant rate about a vertical diameter. Find the height of the bead (in m) above the bottommost point if the angular velocity of rotation is 0.5 rad s-1.

Important Questions on Circular Motion

Learn and Prepare for any exam you want !