A smooth tunnel is dug along a chord of the earth at a perpendicular distance $\frac{R}{2}$ from the centre of the earth where $R=$ radius of the earth. A particle of mass $m$ is released from one end of the tunnel. During the motion of the particle in the tunnel, [$g=$ acceleration due to gravity at the surface of earth]

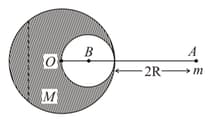
A solid sphere of radius $R$ gravitationally attracts a particle placed at $3R$ from its centre with a force $F_1.$ Now a spherical cavity of radius $\left(\frac{R}{2}\right)$ is made in the sphere (as shown in figure) and the force becomes $F_2$. The value of $F_1:F_2$ is:

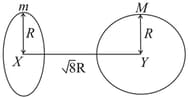
Find the gravitational force of attraction between the ring and sphere as shown in the diagram, where the plane of the ring is perpendicular to the line joining the centres. If $\sqrt{8}R$ is the distance between the centres of a ring (of mass $m$) and a sphere (mass $M$) where both have equal radius $R$

Inside a uniform spherical shell :

(a) The gravitational field is zero.

(b) The gravitational potential is zero.

(c) The gravitational field is the same everywhere.

(d) The gravitation potential is the same everywhere.

(e) All the above.

Choose the most appropriate answer from the options given below:

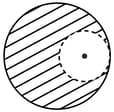
From a solid sphere of mass $M$ and radius $R\text{,}$ a spherical portion of radius $\left(\frac{R}{2}\right)$ is removed as shown in the figure. Taking gravitational potential $V=0$ at $r=\infty ,$ the potential at the centre of the cavity thus formed is ($G=$gravitational constant)

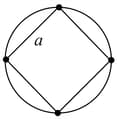
Four identical particles of mass $\mathrm{M}$ are located at the corners of a square of side $‘a’$ . What should be their speed if each of them revolves under the influence of other’s gravitational field in a circular orbit circumscribing the square?

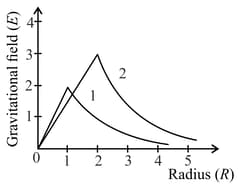
Consider two solid spheres of radii $R_1=1 \mathrm{m}$,$R_2=2 \mathrm{m}$ and masses $M_1$ and $M_2,$ respectively. The gravitational field due to sphere $\left(1\right)$ and $\left(2\right)$ are shown. The value of $\frac{M_1}{M_2}$ is: