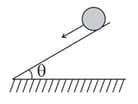
A solid sphere is in pure rolling motion on an inclined surface having inclination , the friction force acting on sphere will be,


Important Questions on Rotational Mechanics
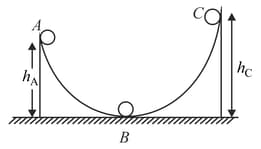
A ball moves over a fixed track as shown in the figure. From the ball rolls without slipping. If surface is frictionless and are kinetic energies of the ball at , respectively, then
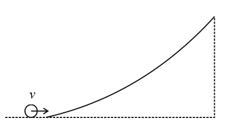
A small object of uniform density rolls up a curved surface with an initial velocity . It reaches up to a maximum height of with respect to the initial position. The object is
Statement-I: Two cylinders, one hollow (metal) and the other solid (wood), with the same mass and identical dimensions, are simultaneously allowed to roll without slipping down an inclined plane from the same height. The hollow cylinder will reach the bottom of the inclined plane first.
and
Statement-2: By the principle of conservation of energy, the total kinetic energies of both the cylinders are identical when they reach the bottom of the incline.
A thin uniform rod, pivoted at , is rotating in the horizontal plane with constant angular speed , as shown in the figure. At times, , a small insect starts from and moves with a constant speed with respect to the rod towards the other end. It reaches the end of the rod at and stops. The angular speed of the system remains throughout. The magnitude of the torque on the system about , as a function of time, is best represented by which plot?
A small mass is attached to a massless string whose other end is fixed at as shown in the figure. The mass is undergoing circular motion is the plane with centre at and constant angular speed . If the angular momentum of the system, calculated about and are denoted by and , respectively, then
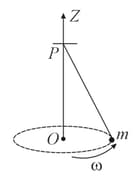
is/(are) correct?
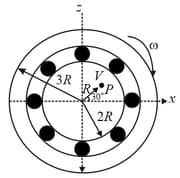
The figure shows a system consisting ofa ring of outer radius rolling clockwise without slipping on a horizontal surface with angular speed and an inner disc of radius rotating anti-clockwise with angular speed The ring and disc are separated frictionless ball bearings. The system is in the The point P on the inner disc is at distance from the origin where makes an angle of with the horizontal. Then with respect to the horizontal surface,
A uniform circular disc of mass and radius is rotating with an angular velocity of about its own axis, which is vertical. Two uniform circular rings, each of mass and radius are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (in ) of the system is
