A solid sphere of radius $R$ is floating in a liquid of density $\rho$ with half of its volume submerged. If the sphere is slightly pushed and released, it starts performing simple harmonic motion. Find the frequency of these oscillations.

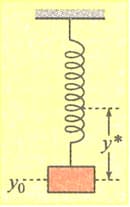
In Fig 22.64 we see a small body, attached to one end of vertically hanging spring, is performing shm about its mean position $y_0$ with angular frequency $\omega$ and amplitude $a$. If at a height $y*$ from the mean position, the body gets detached from the spring, calculate the value of $y*$ so that the height $h$ attained by the mass is maximum. The body does not interact with the spring during its subsequent motion after detachment. ($a{\omega }^2>g$)

A $0.1 \mathrm{kg}$ mass is suspended from a wire of negligible mass. The length of the wire is $1 \mathrm{m}$ and its cross-sectional area is $4.9\times {10}^{-7}{\mathrm{m}}^2$. If the mass is pulled a little in the vertically downward direction and released, it performs simple harmonic motion of angular frequency $140 \mathrm{rad} {\mathrm{s}}^{-1}$. If the Young’s modulus of the material of the wire is $n\times {10}^9 \mathrm{N} {\mathrm{m}}^{-2}$, the value of $n$ is

Two identical springs of constant $k$ are connected in first series and then in parallel. A mass $m$ is suspended from them. The ratio of their frequencies of vertical oscillations is

A particle executes simple harmonic motion between $x=-A$ and $x=+A$. The time taken by it to go from $0$ to $\frac{A}{2}$ is $T_1$ and to go from $\frac{A}{2}$ to $A$ is $T_2$. Then

A body executes simple harmonic motion. The potential energy (PE), kinetic energy (KE) and total energy (TE) are measured as a function of displacement ($x$). Which of the following statements is true?

A pendulum is suspended in a lift. When the lift accelerates upward with an acceleration $a$, its time period is $T_1$; when the lift, accelerates downward with the same acceleration, its time period is $T_2$. Which of the following relations hold true?

The maximum velocity of a particle, executing SHM with an amplitude $7 \mathrm{mm}$ is $4.4 {\mathrm{ms}}^{-1}$. The period of oscillation is