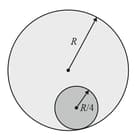
A solid sphere rolls on a smooth horizontal surface at $10 \mathrm{m}/\mathrm{s}$ and then rolls up a smooth inclined plane of inclination $30°$ with horizontal. The mass of the sphere is $2 \mathrm{kg}$. Find the height attained by the sphere before it stops (in $m$ ).

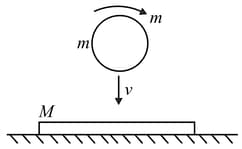
A solid ball of mass $m$ and radius $r$ spinning with angular velocity $\omega$ falls on a horizontal slab of mass $M$ with rough upper surface (coefficient of friction $\mu$) and smooth lower surface. Immediately after collision the normal component of velocity of the ball remains half of its value just before collision and it stops spinning. Find the velocity of the sphere in horizontal direction immediately after the impact (given: $R\omega =5$).

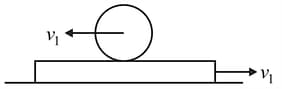
A sphere of radius $r$ and mass $m$ has a linear velocity $v_0 \mathrm{m}/\mathrm{s}$ directed to the left and no angular velocity as it is placed on a horizontal platform moving to the right with a constant velocity $10 \mathrm{m}/\mathrm{s}$. If after sliding on the platform the sphere is to have no linear velocity relative to the ground as it starts rolling on the platform without sliding. The coefficient of kinetic friction between the sphere and the platform is ${\mu }_k$ Determine the required value of $v_0$ in $\mathrm{m}/\mathrm{s}.$

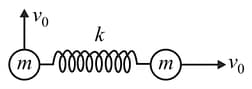
Two small spheres of mass $1 \mathrm{kg}$ each are connected to each other by means of an unstretched spring of force constant $k=100 \mathrm{N}/\mathrm{m}$ and natural length $2.4 \mathrm{m}.$The system is placed on a smooth horizontal surface and the two spheres are given velocities $v_0,$ as shown in the figure. The maximum elongation in the spring is found to be $0.4 \mathrm{m}$ during the subsequent motion. Calculate $v_0$ in $\mathrm{m}/\mathrm{s}.$ Take $\sqrt{31}=5.6$

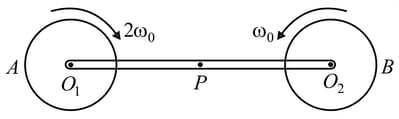
A rod of mass '$M$' and length $6 R$ is pivoted at its centre (point $P$) to rotate in vertical plane as shown. Two discs of same radius $\text{'}R\text{'}$ are joined at the ends $O,$ and $O_2$ of the rod. Mass of the discs $A$ and $B$ are $\text{'}M$ and $\text{'}2M\text{'}$ respectively. Initial angular velocities of discs are shown in figure. The system is released from rest from horizontal position. Find the angular velocity of the $\mathit{rod}$ (in $\mathrm{rad} {\sec }^{-1}$)when it is vertical. (Given $R=0.5 \mathrm{m}$ and $g=10 {\mathrm{ms}}^{-2}$)