A heat exchanger of length l consists of a tube of cross-sectional area 2 S with another tube of cross-sectional area S passing through it (Fig). The walls of the tubes are thin. The entire system is thermally insulated from the ambient. A liquid of density ρ and specific heat c is pumped at a velocity v through the tubes. The initial temperatures of the liquid in the heat exchanger are T 11 and T 12 respectively. Determine the final temperatures T f 1 and T f 2 of the liquid in the heat exchanger if the liquid passes through the tubes in the counterflow, assuming that the heat transferred per unit time through a unit area element is proportional to the temperature difference, the proportionality factor being k . The thermal conductivity of the liquid in the direction of its flow should be neglected.

For definiteness, we shall assume that the liquid flowing in the inner tube 2 is cooled, i.e. T i 2 > T f 2 , and hence T i 1 < T f 1 . Since the cross-sectional area 2 S - S = S of the liquid flow in the outer tube 1 is equal to the cross-sectional area S of the liquid flow in the inner tube 2 , and their velocities coincide, the decrease in temperature of the liquid flowing in the tube 2 from the entrance to the exit is equal to the decrease in temperature of the liquid flowing in the tube 1 . In other words, the temperature difference in the liquids remains constant along with the heat exchanger, and hence T i 2 - T f 1 = T f 2 - T i 1 . . . . 1 Given the constancy of the temperature difference, the rate of heat transfer is constant along with the heat exchanger. The amount of heat Q transferred from the liquid flowing in a tube 2 to the liquid flowing in the tube 1 during a time t is Q = S 1 at k t T i 2 - T f 1 . . . . . 2 . Here S 1 at is the lateral surface of the inner tube, S 1 at = 2 π r l , where r is the radius of the inner tube, i.e. π r 2 = S , and r = S π . The a mount of heat Q is spent for heating the liquid flowing in tube 1 . During the time t , the mass of the liquid flowing in the outer tube 1 is m = ρ v t S , and its temperature increases from T i 1 to T f 1 . Consequently, Q = ρ v t S c T f 1 - T i 1 . . . . 3 Equating expressions 2 and 3 , we obtain 2 π ∇ S ¯ π l k T i 2 - T f 1 = ρ v S c T f 1 - T i 1 . Hence we can find T f 1 , and using Eq : 1 , T f 2 as well. Therefore, we can write T P 1 = T i 2 + T i 1 - T i 2 1 + 2 π S l k ρ v c - 1 T f 2 = T i 1 + T i 2 - T i 1 1 + 2 π S l k ρ v c - 1

A vessel of volume V = 21 contains m H 2 = 2 g of hydrogen and some amount of water. The pressure in the vessel is p 1 = 17 × 10 5 Pa . The vessel is heated so that the pressure in it increases to p f = 26 × 10 5 Pa , and water partially evaporates. The molar mass of water vapour is μ = 18 × 10 - 3 kg mol - 1 . Determine the initial T 1 and final T f temperature of water and its mass Δ m . T , C ∘ 100 120 133 152 180 p sat × 10 6 Pa 1 2 3 5 10

The total pressure p in the vessel is the sum of the saturated water vapour pressure p sat and the pressure of hydrogen p H 2 . According to the equation of state for an ideal gas, the pressure of hydrogen is , p H 2 = m i H 3 μ H 3 V R T = 2 × 10 - 3 kg × S . 3 J mol K - 1 2 × 10 - 3 kg mol - 1 × 2 × 10 - 3 in 3 T = 4 . 15 × 10 3 T , where p H 2 is measured in pascals. The p H I 2 T dependence is linear. Therefore, having calculated p H , T for two values of temperature, say, for T 1 = 373 K , p H 2 = 15 . 5 × 10 5 Pa T 2 = 453 K , p H 2 = 18 . 8 × 10 5 Pa we plot the graph of p H 3 T . Using the hint in the conditions of the problem, we plot the graph of the function p sat T . "Composing" the graphs of p H 2 T and p sat T , we obtain the graph of the temperature dependence of the total pressure in the vessel, p T (Fig). Using the p T curve, from the initial and final values of pressure specified in the conditions of the problem, we obtain the initial and final tempera tures in the vessel: p 1 = 17 × 10 5 Pa , T 1 = T 1 ≃ 380 K p f = 26 × 10 5 Pa , T 2 = T f ≃ 440 K Let us now determine the mass of evaporated water. Assuming that water vapour is an ideal gas, we calculate the initial p v 1 and final p v 2 pressures of water vapour in the vessel. For this purpose, we make use of the obtained graphs. For T 1 = 380 K , the pressure of hydrogen is p H 2 ' ≃ 15 . 5 × 10 ° Pa , and p v 1 = p 1 - p H 2 ' ≃ 1 . 5 × 10 5 Pa . For T 2 = 440 K , p H 2 ' ' ≃ 18 × 10 5 Pa , and p v 2 = p f - p H 2 ' ' ≃ 8 × 10 5 Pa . p v 2 = p f - p H 2 ' ' ≃ 8 × 10 5 Pa . Let us write the equations of state for water vapour at p v 1 , T 1 and p v 2 , T 2 : p v 1 V = m v 1 μ v R T 1 , p v 2 V = m v 2 μ v R T 2 , where m v 1 and m v 2 are the initial and final masses of vapour in the vessel. Hence we can determine the mass of evaporated water: Δ m = m v 2 - m v 1 = μ v V R p v 2 T 2 - p v 1 T 1 = 18 × 10 - 3 kg mol - 1 × 2 × 10 - 3 m 3 8 . 3 J K · mol - 1 × 8 Pa 440 K - 1 . 5 Pa 380 K × 10 5 = 6 × 10 - 3 kg = 6 g .

HARD

JEE Advanced

IMPORTANT

Earn 100

A space object has the shape of a sphere of radius $R$ . Heat sources ensuring the heat evolution at a constant rate are distributed uniformly over its volume. The amount of heat liberated by a unit surface area is proportional to the fourth power of thermodynamic temperature.

In what proportion would the temperature of the object change if its radius decreased by half?

Important Questions on Heat and Molecular Physics

HARD

JEE Advanced

IMPORTANT

Science for Everyone Aptitude test problems in Physics>Chapter 2 - Heat and Molecular Physics>Exercise>Q 2.18

A heat exchanger of length $l$ consists of a tube of cross-sectional area $2 S$ with another tube of cross-sectional area $S$ passing through it (Fig). The walls of the tubes are thin. The entire system is thermally insulated from the ambient. A liquid of density $ρ$ and specific heat $c$ is pumped at a velocity $v$ through the tubes. The initial temperatures of the liquid in the heat exchanger are $T_{11}$ and $T_{12}$ respectively.

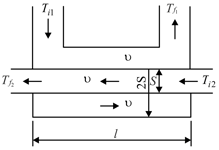
Question Image

Determine the final temperatures $T_{f_{1}}$ and $T_{f_{2}}$ of the liquid in the heat exchanger if the liquid passes through the tubes in the counterflow, assuming that the heat transferred per unit time through a unit area element is proportional to the temperature difference, the proportionality factor being $k$ . The thermal conductivity of the liquid in the direction of its flow should be neglected.

HARD

JEE Advanced

IMPORTANT

Science for Everyone Aptitude test problems in Physics>Chapter 2 - Heat and Molecular Physics>Exercise>Q 2.19

A closed cylindrical vessel of base area $S$ contains a substance in the gaseous state outside the gravitational field of the Earth. The mass of the gas is $M$ and its pressure is $p$ such that $p ≪ p_{sat}$ , where $p_{sat}$ is the saturated vapour pressure at a given temperature. The vessel starts moving with an acceleration $a$ directed along the axis of the cylinder. The temperature is maintained constant.

Determine the mass $m_{11 q}$ of the liquid condensed as a result of motion in the vessel.

HARD

JEE Advanced

IMPORTANT

Science for Everyone Aptitude test problems in Physics>Chapter 2 - Heat and Molecular Physics>Exercise>Q 2.2

The saturated water vapour pressure on a planet is

p_{0} = 760 mm Hg

. Determine the vapour density

ρ

HARD

JEE Advanced

IMPORTANT

Science for Everyone Aptitude test problems in Physics>Chapter 2 - Heat and Molecular Physics>Exercise>Q 2.21

In cold weather, water vapour can be seen in the exhaled air. If the door of a warm hut is opened on a chilly day, fog rushes into the hut. Explain these phenomena.

HARD

JEE Advanced

IMPORTANT

Science for Everyone Aptitude test problems in Physics>Chapter 2 - Heat and Molecular Physics>Exercise>Q 2.22

A vessel of volume $V = 21$ contains $m_{H_{2}} = 2 g$ of hydrogen and some amount of water. The pressure in the vessel is $p_{1} = 17 \times 10^{5} Pa$ . The vessel is heated so that the pressure in it increases to $p_{f} = 26 \times 10^{5} Pa$ , and water partially evaporates. The molar mass of water vapour is $μ = 18 \times 10^{- 3} kg {mol}^{- 1}$ . Determine the initial $T_{1}$ and final $T_{f}$ temperature of water and its mass $Δ m$ .

$T, {}^{\circ}C$	$100$	$120$	$133$	$152$	$180$
$p_{sat} \times 10^{6} Pa$	$1$	$2$	$3$	$5$	$10$

HARD

JEE Advanced

IMPORTANT

Science for Everyone Aptitude test problems in Physics>Chapter 2 - Heat and Molecular Physics>Exercise>Q 2.23

The lower end of a capillary of radius $r = 0.2 mm$ and length $l = 8 cm$ is immersed in water whose temperature is constant and equal to $T_{low} = 0 ° C$ . The temperature of the upper end of the capillary is $T_{up} = 100 ° C$ .

Determine the height $h$ to which the water in the capillary rises, assuming that the thermal conductivity of the capillary is much higher than the thermal conductivity of water in it. The heat exchange with the ambient should be neglected.

$T, ° C$	$0$	$20$	$50$	$90$
$a, mN m^{- 1}$	$76$	$73$	$67$	$60$

HARD

JEE Advanced

IMPORTANT

Science for Everyone Aptitude test problems in Physics>Chapter 2 - Heat and Molecular Physics>Exercise>Q 2.24

A cylinder with a movable piston contains air under a pressure

p_{1}

and a soap bubble of radius

r

. The surface tension is

σ

, and the temperature

T

is maintained constant. Determine the pressure

p_{2}

to which the air should be compressed by slowly pulling the piston into the cylinder for the soap bubble to reduce its size by half.

HARD

JEE Advanced

IMPORTANT

Science for Everyone Aptitude test problems in Physics>Chapter 2 - Heat and Molecular Physics>Exercise>Q 2.25

Why is clay used instead of cement (which has a higher strength) in laying bricks for a fireplace?

Important Questions on Heat and Molecular Physics

Learn and Prepare for any exam you want !