A sphere of mass $m$ suspended by a thread of length $‘l’$ is oscillating in a vertical plane, the angular amplitude being ${\mathrm{\theta }}_0$. What is the tension in the thread when it makes an angle $\mathrm{\theta }$ with the vertical during oscillations? If the thread can support a maximum tension of $2 \mathrm{mg}$, then what can be the maximum angular amplitude of oscillation of the sphere without breaking the rope?

A machine, in an amusement park, consists of a cage at the end of one arm, hinged at $O$. The cage revolves along a vertical circle of radius $r$ $\left(\mathrm{ABCDEFGH}\right)$ about its hinge $O$, at constant linear speed $v=\sqrt{gr}$ . The cage is so attached that the man of weight $w$ standing on a weighing machine, inside the cage, is always vertical. Then which of the following is/are correct.

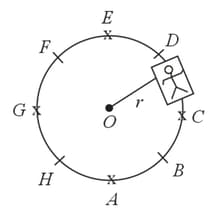
(I) $h=0.1 \mathrm{m} \mathrm{and} \mathrm{cos\theta }=\frac{2}{3}$.

(II) $h=0.2 \mathrm{m} \mathrm{and} \mathrm{cos\theta }=\frac{1}{3}$

(III)$v =2\sqrt{ 2} \mathrm{m} {\mathrm{s}}^{–1}$.

(IV) After leaving the circular track the particle will describe a parabolic path. Therefore,

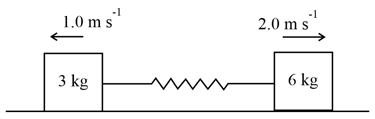
Two blocks of mass $3 \mathrm{kg}$ and $6 \mathrm{kg}$ respectively are placed on a smooth horizontal surface. They are connected by a light spring of force constant $k=200 \mathrm{N} {\mathrm{m}}^{-1}.$ Initially the spring is unstretched and the indicated velocities are imparted to the blocks. Find maximum extension of the spring in $\mathrm{cm}$ ?

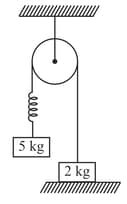
The system as shown in the figure is released from rest. The pulley, spring and string are ideal & friction is absent everywhere. If the speed of $5 \mathrm{kg}$ block when $2 \mathrm{kg}$ block leaves the contact with ground is $2\sqrt{x }\mathrm{m} {\mathrm{s}}^{-1},$ then the valu thee of $x$ is : (spring constant $k\mathit{=} 40 \mathrm{N} {\mathrm{m}}^{-1}$ and $g = 10 \mathrm{m} {\mathrm{s}}^{-2})$

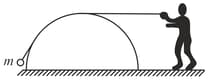
As shown in the figure a person is pulling a mass $\text{'}m\text{'}$ from the ground on a fixed rough hemispherical surface up to the top of the hemisphere with the help of a light inextensible string. Find the work done (in Joules) by tension in the string on mass $m$ if radius of the hemisphere is $R$ and the friction coefficient is $\mathrm{\mu }$. Assume that the block is pulled with negligible velocity. (Take $\mathrm{\mu } = 0.1, m= 1\mathrm{kg}, g=10 \mathrm{m} {\mathrm{s}}^{-2}, R=1 \mathrm{m}$).

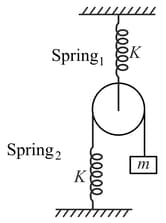
All springs, string and pulley shown in the figure are light. Initially, when both the springs were in their natural state, the system was released from rest. The maximum displacement of the block $\mathrm{m}$ is $x \times \left(\frac{5mg}{k}\right)$ Calculate $x\mathit{.}$

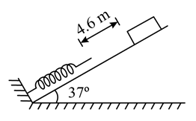
As shown in the figure, a spring is fixed at the bottom end of an inclined plane of inclination $37°$. A block of mass $4 \mathrm{kg}$ starts slipping down the incline from a point $4.6 \mathrm{m}$ away from the spring. The block compresses the spring by $40 \mathrm{cm}$, stops momentarily and then rebounds through a distance of $3 \mathrm{m}$ up the incline. If the spring constant of the spring is $\frac{{10}^{3}x}{8} \mathrm{N} {\mathrm{m}}^{-1}$, then the value of $x$ is (take $g=10 \mathrm{m} {\mathrm{s}}^{-2}$),