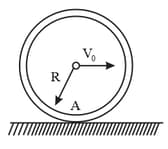
A spool, with a thread wound on it, of mass , rests on a rough horizontal surface. Its moment of inertia, relative to its own axis, is equal to, , where is a numerical factor and is the outside radius of the spool. The radius of the wound thread layer is equal to . The spool is pulled, without sliding, by the thread, with a constant force , directed at an angle to the horizontal. Find:
the projection of the acceleration vector of the spool axis, on the -axis;
the work performed by the force , during the first , after the beginning of the motion.
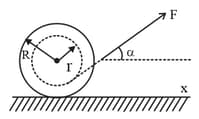
the projection of the acceleration vector of the spool axis, on the -axis;
the work performed by the force , during the first , after the beginning of the motion.


Important Questions on PHYSICAL FUNDAMENTALS OF MECHANICS
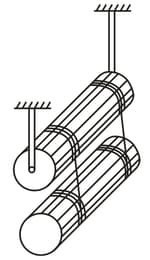
The arrangement shown in figure consists of two identical uniform solid cylinders, each of mass , on which two light threads are wound symmetrically. Find the tension of each thread in the process of motion. The friction in the axle of the upper cylinder is assumed to be absent.
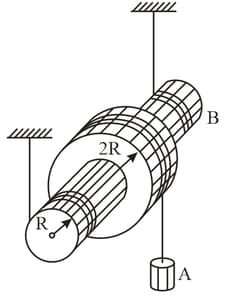
In the arrangement shown in the figure, a weight , possesses mass . A pulley , possesses mass . Also known are the moment of inertia , of the pulley relative to its axis and the radii of the pulley and . The mass of the threads is negligible. Find the acceleration of the weight , after the system is set free.
A uniform solid cylinder , of mass , can freely rotate about a horizontal axis fixed to a mount , of mass . A constant horizontal force , is applied to the end , of a light thread tightly wound on the cylinder. The friction between the mount and the supporting horizontal plane is assumed to be absent. Find:
the acceleration of the point
the kinetic energy of this system, after the beginning of motion.
A plank of mass , with a uniform sphere of mass placed on it, rests on a smooth horizontal plane. A constant horizontal force is applied to the plank. With what accelerations will the plank and the centre of the sphere move, provide there is no sliding between the plank and the sphere?
how long the cylinder will move with sliding;
the total work performed by the sliding friction force acting on the cylinder.
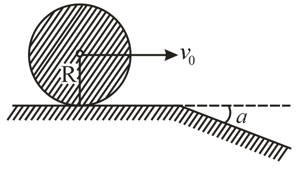
A uniform solid cylinder of radius , rolls over a horizontal plane, passing into an inclined plane, forming an angle , with the horizontal. Find the maximum value of the velocity , which still permits the cylinder to roll onto the inclined plane section, without a jump. The sliding is assumed to be absent.
A small body is fixed to the inside of a thin rigid hoop, of radius and mass equal to that of the body . The hoop rolls, without slipping, over a horizontal plane. At the moment when the body gets into the lower position, the centre of the hoop moves with a velocity . At what values of , will the hoop move without bouncing?