A square loop of side carries a current . Calculate magnetic induction at point , lying on the axis of loop and at a distance from the center of loop.
Important Questions on Moving Charges and Magnetism
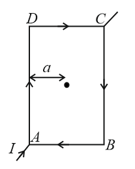
A square loop, carrying a steady current , is placed in a horizontal plane near a long straight conductor carrying a steady current at a distance from the conductor as shown in the figure. The loop will experience
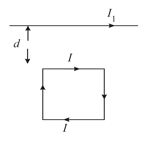
In the given figure, the magnetic field at .
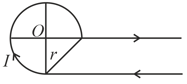
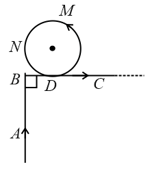
[Take ]
The current in flowing along the path of a cube (shown in the left figure) produces a magnetic field at the centre of cube of magnitude . Dashed line depicts the non-conducting part of the cube.
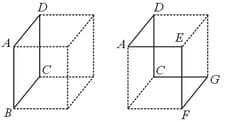
Consider a cubical shape shown to the right which is identical in size and shape to the left. If the same current now flows in along the path , then the magnitude of magnetic field at the centre will be
A square loop is made from a uniform wire as shown in the figure. If a battery is connected between the points then the magnitude of the magnetic field at the center of the square is