A stopper is inserted in a small hole of the glass tube of the mercury barometer below the top level of the mercury in it. What happens when you pull out the stopper from the glass tube?

A cylindrical vessel containing a liquid is rotated about its axis so that the liquid rises at its sides as shown in the figure. The radius of vessel is $5 \mathrm{cm}$ and the angular speed of rotation is $\mathrm{\omega } \mathrm{rad} {\mathrm{s}}^{-1}$. The difference in the height, $\mathrm{h} \left(\mathrm{in} \mathrm{cm}\right)$ of liquid at the Centre of vessel and at the sides of the vessel will be :

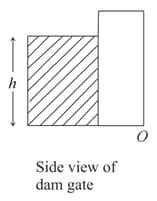
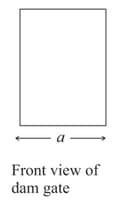
Water stands upto height $\text{'}h\text{'}$ behind the dam as shown in the figure. The front view of the dam gate is also shown in the adjoining figure. Density of water is $\text{'}\rho \text{'}$ and acceleration due to gravity is $\text{'}g\text{'}$. If atmospheric pressure force is also considered, the point of application of total force acting on the dam due to water above $\text{'}o\text{'}$ is_____

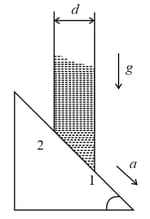
A cylindrical tube, with its base as shown in the figure., is filled with water. It is moving down with a constant acceleration $a$ along a fixed inclined plane with angle $\theta =45°$. $P_1$ and $P_2$ are pressures at point $1$ and $2$, respectively, located at the base of the tube. Let $\beta =\frac{\left(P_1-P_2\right)}{\left(\rho gd\right)}$, where $\rho$ is density of water, $d$ is the inner diameter of the tube and $g$ is the acceleration due to gravity. Which of the following statement(s) is (are) correct?

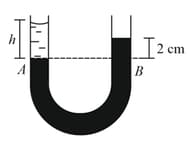
The liquid shown in the figure in the two arms is mercury (specific gravity $13.6$) and water. If the difference of heights of the mercury column is $2 \mathrm{cm}$, the height $h$ of the water column is

A barometer is constructed using a liquid (density $=760 \mathrm{kg} {\mathrm{m}}^{-3}$). What would be the height of the liquid column, when a mercury barometer reads $76 \mathrm{cm}?$

(density of mercury $=13600 \mathrm{kg} {\mathrm{m}}^{-3}$)

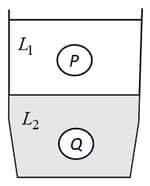
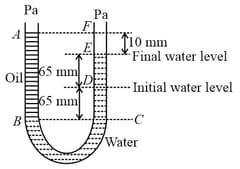
An open-ended U-tube of uniform cross-sectional area contains water (density ${10}^3 \mathrm{kg} {\mathrm{m}}^{-3}$ ). Initially the water level stands at $0.29 \mathrm{m}$ from the bottom in each arm. Kerosene oil (a water-immiscible liquid) of density $800 \mathrm{kg} {\mathrm{m}}^{-3}$ is added to the left arm until its length is $0.1 \mathrm{m}$, as shown in the schematic figure below. The ratio $\left(\frac{h_1}{h_2}\right)$ of the heights of the liquid in the two arms is

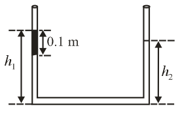
Two liquids of densities ${\rho }_1$ and ${\rho }_2\left({\rho }_2=2{\rho }_1\right)$ are filled up behind a square wall of side $10 \mathrm{m}$ as shown in figure. Each liquid has a height of $5 \mathrm{m}.$ The ratio of the forces due to these liquids exerted on upper part $MN$ to that at the lower part $NO$ is (Assume that the liquids are not mixing):