A student travels to college by either of two routes, or . The probability that they use route is , and the probability that they are passed by a bus on their way to college on any particular day is . They are twice as likely to be passed by a bus when they use route as when they use route .
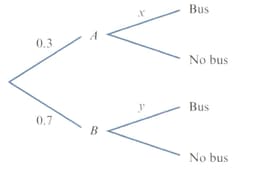
Find the probability that the student uses route , given that they are not passed by a bus on their way to college. [correct up to three decimal places]


Important Questions on Probability
Two ordinary fair dice are rolled. If the first shows a number less than , then the score is the mean of the numbers obtained; otherwise the score is equal to half the absolute (non-negative) difference between the numbers obtained. Find the probability that the score is:
positive
Two ordinary fair dice are rolled. If the first shows a number less than , then the score is the mean of the numbers obtained; otherwise the score is equal to half the absolute (non-negative) difference between the numbers obtained. Find the probability that the score is:
greater than , given that it is less than
Two ordinary fair dice are rolled. If the first shows a number less than , then the score is the mean of the numbers obtained; otherwise the score is equal to half the absolute (non-negative) difference between the numbers obtained. Find the probability that the score is:
less than , given that it is greater than
Three friends, Rick, Brenda and Ali, go to a football match but forget to say which entrance to the ground they will meet at. There are four entrances, and . Each friend chooses an entrance independently.
- The probability that Rick chooses entrance is The probabilities that he chooses entrances or are all equal.
- Brenda is equally likely to choose any of the four entrances.
- The probability that Ali chooses entrance is and the probability that he chooses entrance is . The probabilities that he chooses the other two entrances are equal.
Find the probability that at least friends will choose entrance .
Three friends, Rick, Brenda and Ali, go to a football match but forget to say which entrance to the ground they will meet at. There are four entrances, and . Each friend chooses an entrance independently.
- The probability that Rick chooses entrance is The probabilities that he chooses entrances or are all equal.
- Brenda is equally likely to choose any of the four entrances.
- The probability that Ali chooses entrance is and the probability that he chooses entrance is . The probabilities that he chooses the other two entrances are equal.
Find the probability that the three friends will all choose the same entrance. [correct up to three decimal places]
Maria chooses toast for her breakfast with probability . If she does not choose toast then she has a bread roll. If she chooses toast then the probability that she will have jam on it is . If she has a bread roll then the probability that she will have jam on it is .
Draw a fully labelled tree diagram to show this information.
Maria chooses toast for her breakfast with probability . If she does not choose toast then she has a bread roll. If she chooses toast then the probability that she will have jam on it is . If she has a bread roll then the probability that she will have jam on it is .
Given that Maria did not have jam for breakfast, find the probability that she had toast. [correct up to three decimal places]
Ronnie obtained data about the gross domestic product (GDP) and the birth rate for countries. He classified each GDP and each birth rate as either 'low', 'medium' or 'high'. The table shows the number of countries in each category.
| Birth rate | ||||
| Low | Medium | High | ||
| GDP | Low | |||
| Medium | ||||
| High |
One of these countries is chosen at random.
Find the probability that the country chosen has a medium GDP. [correct up to three decimal places]
