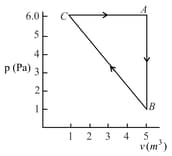
A thermodynamic system is taken from an original state to an intermediate state by a linear process as shown in the figure. Its volume is then reduced to the original value from to by an isobaric process. The total work done by the gas from to and to would be :

Important Questions on Thermodynamics
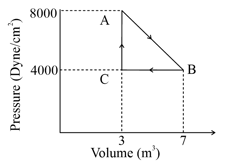
One mole of an ideal diatomic gas undergoes a transition from to along a path as shown in the figure,
The change in internal energy of the gas during the transition is:
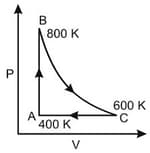
One mole of diatomic ideal gas undergoes a cyclic process ABC as shown in figure. The process BC is adiabatic. The temperatures at A, B and C are 400 K, 800 K and 600 K respectively. Choose the correct statement :
(Take gas constant )
(Take , where is gas constant)
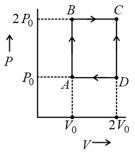
An ideal gas is taken reversibly around the cycle as shown on the T (temperature) - S (entropy) diagram
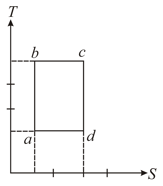
The most appropriate representation of above cycle on a U (internal energy)-V (volume) diagram is
Thermodynamic processes are indicated in the following diagram.
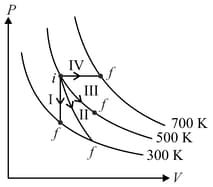
Match the following
| Column – 1 | Column - 2 |
| P. Process I | a. Adiabatic |
| Q. Process II | b. Isobaric |
| R. Process III | c. Isochoric |
| S. Process IV | d. Isothermal |
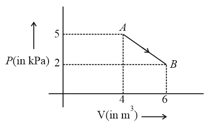
For the given cyclic process as shown for a gas, the work done is: