A thin non-conducting ring of radius has a linear charge density , where is a constant, is the azimuthal angle. Find the magnitude of the electric field strength,
(a) at the centre of the ring,
(b) on the axis of the ring as a function of the distance from its centre. Investigate the obtained function at .

Important Questions on Electrostatics
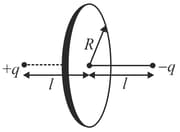
Two point charges are separated by the distance (figure). Find the flux of the electric field strength vector across a circle of radius .
Four point charges and are fixed at the points, and respectively on the A particle of mass and of charge moves along the direction. Its speed at is Find the least value of for which the particle will cross the origin. Find also the kinetic energy of the particle at the origin. Assume that space is gravity-free. Given:
