A thin superconducting ring is held above a vertical long solenoid as shown in the figure. Axis of solenoid is same as that of a ring. The cylindrically symmetric magnetic field around the ring in terms of vertical and radial component, is $B_z=B_0\left(1-\alpha z\right)$ and $B_r=B_{0}Br$ where $B_0, \alpha$ and $B$ are positive constant and $z$ and $r$ are vertical and radial components respectively. Initially plane of ring is horizontal with no current flowing through it. Mass of the ring is $m$, radius $r_0$ and self inductance $L.$ If initially, coordinates of ring are $\left(0, 0, 0\right)$ and it is released then

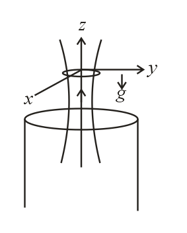
When the ring is at vertical position $z$, then current in the ring is $\frac{k{B}_0\alpha z\pi r_0^2}{L}.$ Find constant $k$ in current expression.

In the following part of a circuit $i_1=5 A,\frac{d{l}_1}{dt}=3A{s}^{-1},i_2=2 A,\frac{d{i}_2}{dt}=-4 A/s$. Find $V_A-V_B .$

Find time constant for following circuits.

 (a) (b) 

(c)  (d)

Switch was in position $1$ for a long time. It is suddenly switch to position $2$. Find voltage drop across inductor immediately after the switch is toggled.

A thin superconducting ring is held above a vertical long solenoid as shown in the figure. Axis of solenoid is same as that of a ring. The cylindrically symmetric magnetic field around the ring in terms of vertical and radial component, is $B_z=B_0\left(1-\alpha z\right)$ and $B_r=B_{0}Br$ where $B_0, \alpha$ and $B$ are positive constant and $z$ and $r$ are vertical and radial components respectively. Initially plane of ring is horizontal with no current flowing through it. Mass of the ring is $m$, radius $r_0$ and self inductance $L.$ If initially, coordinates of ring are $\left(0, 0, 0\right)$ and it is released then

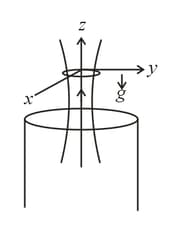
If ring is at equilibrium at vertical coordinate $z=-\frac{mgL}{2B_0^2\alpha B{\pi }^2{r}_0^N}$, then value of $N$ (Power of $r_0$) is

A thin superconducting ring is held above a vertical long solenoid as shown in the figure. Axis of solenoid is same as that of a ring. The cylindrically symmetric magnetic field around the ring in terms of vertical and radial component, is $B_z=B_0\left(1-\alpha z\right)$ and $B_r=B_{0}Br$ where $B_0, \alpha$ and $B$ are positive constant and $z$ and $r$ are vertical and radial components respectively. Initially plane of ring is horizontal with no current flowing through it. Mass of the ring is $m$, radius $r_0$ and self inductance $L.$ If initially, coordinates of ring are $\left(0, 0, 0\right)$ and it is released then

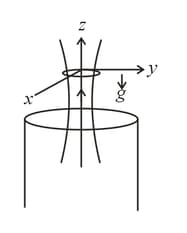
If tension in the ring is maximum when $z=\frac{1}{c\alpha }$, then value of $c$ is