MEDIUM
10th Tamil Nadu Board
IMPORTANT
Earn 100

A toy is in the shape of a cylinder surmounted by a hemisphere. The height of the toy is 25 cm. Find the total surface area of the toy if its common diameter is 12 cm.

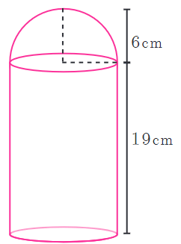
Question Image

Important Questions on Mensuration

EASY
10th Tamil Nadu Board
IMPORTANT
Mathematics Standard 10>Chapter 7 - Mensuration>Progress Check>Q 2
In a right circular cylinder the axis is _____ to diameter.     
MEDIUM
10th Tamil Nadu Board
IMPORTANT
Mathematics Standard 10>Chapter 7 - Mensuration>Progress Check>Q 2
In a right circular cone the axis is _____ to the diameter.
MEDIUM
10th Tamil Nadu Board
IMPORTANT
Mathematics Standard 10>Chapter 7 - Mensuration>Thinking Corner>Q 1
Find the value of the radius of a sphere whose surface area is 36π sq. units.
EASY
10th Tamil Nadu Board
IMPORTANT
Mathematics Standard 10>Chapter 7 - Mensuration>Thinking Corner>Q 2
How many great circles can a sphere have?
EASY
10th Tamil Nadu Board
IMPORTANT
Mathematics Standard 10>Chapter 7 - Mensuration>Thinking Corner>Q 3
Find the surface area of the earth whose diameter is 12756 kms. (Use π=227)
EASY
10th Tamil Nadu Board
IMPORTANT
Mathematics Standard 10>Chapter 7 - Mensuration>Progress Check>Q 1
Every section of a sphere by a plane is a _____.
EASY
10th Tamil Nadu Board
IMPORTANT
Mathematics Standard 10>Chapter 7 - Mensuration>Progress Check>Q 2
The centre of a great circle is at the _____ of the sphere.
EASY
10th Tamil Nadu Board
IMPORTANT
Mathematics Standard 10>Chapter 7 - Mensuration>Progress Check>Q 3
Find the difference between the T.S.A. and C.S.A. of hemisphere.