HARD
AS and A Level
IMPORTANT
Earn 100

A train consists of an engine and five carriages. The engine has mass 100000 kg and each carriage has mass 20000 kg. The engine produces a driving force of 350000 N. The resistance force on the engine is 10000 N and the resistance on each carriage is 2000 N. The train moves in a straight line on a horizontal track. Find the tension in the coupling between the third carriage and the fourth carriage. Take g=10 m s-2.
 

Important Questions on Connected Particles

HARD
AS and A Level
IMPORTANT
Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 5 - Connected Particles>EXERCISE 5A>Q 10
A car pulls a caravan up a hill. The slope of the hill makes an angle $\theta$ with the horizontal, where sinθ=120. The car has mass 1900 kg and the caravan has mass 600 kg. The driving force from the engine of the car is 1200 N. The resistance on the car is 20 N and that on the caravan is 80 N. Find the force in the tow-bar and state whether it is a tension force or a thrust force. Take g=10 m s-2.
 
HARD
AS and A Level
IMPORTANT
Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 5 - Connected Particles>EXERCISE 5A>Q 11
A car tows a caravan down a hill. The slope of the hill makes an angle θ with the horizontal, where sinθ=120. The car has mass 1900 kg and the caravan has mass 600 kg. The car is braking, so the driving force from the engine of the car is negative. This braking force is 250 N (a driving force of -250 N). The resistance on the car is 20 N and that on the caravan is 80 N. Find the force in the tow-bar and state whether it is a tension force or a thrust force. Take g=10 m s-2.
HARD
AS and A Level
IMPORTANT
Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 5 - Connected Particles>EXERCISE 5A>Q 12
A car tows a caravan down a hill. The slope of the hill makes an angle θ with the horizontal, where sinθ=0.05. The force from the car's engine is a braking force (a negative driving force). The car has mass 1800 kg and the caravan has mass 600 kg. The resistance on the car is 20 N and that on the caravan is 80 N. The force in the tow-bar is a thrust of 50 N. Show that the force from the car's engine is -420 N. Take g=10 m s-2.
MEDIUM
AS and A Level
IMPORTANT
Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 5 - Connected Particles>EXERCISE 5B>Q 1

In each of the following diagrams, the blocks are at rest and are connected by light strings passing over smooth pulleys. Any hanging portion of a string is vertical and any other portion is parallel to the surface. Unless marked otherwise, the surfaces are rough and horizontal. In each case, find the magnitude of the tension in each string and the magnitude of any frictional force.

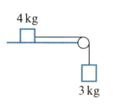
Question Image

MEDIUM
AS and A Level
IMPORTANT
Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 5 - Connected Particles>EXERCISE 5B>Q 1

In each of the following diagrams, the blocks are at rest and are connected by light strings passing over smooth pulleys. Any hanging portion of a string is vertical and any other portion is parallel to the surface. Unless marked otherwise, the surfaces are rough and horizontal. In each case, find the magnitude of the tension in each string and the magnitude of any frictional force.

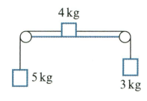
Question Image

MEDIUM
AS and A Level
IMPORTANT
Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 5 - Connected Particles>EXERCISE 5B>Q 1

In each of the following diagrams, the blocks are at rest and are connected by light strings passing over smooth pulleys. Any hanging portion of a string is vertical and any other portion is parallel to the surface. Unless marked otherwise, the surfaces are rough and horizontal. In each case, find the magnitude of the tension in each string and the magnitude of any frictional force.

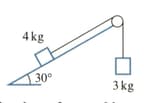
Question Image

MEDIUM
AS and A Level
IMPORTANT
Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 5 - Connected Particles>EXERCISE 5B>Q 1

In each of the following diagrams, the blocks are at rest and are connected by light strings passing over smooth pulleys. Any hanging portion of a string is vertical and any other portion is parallel to the surface. Unless marked otherwise, the surfaces are rough and horizontal. In each case, find the magnitude of the tension in each string and the magnitude of any frictional force.

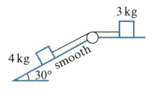
Question Image

MEDIUM
AS and A Level
IMPORTANT
Cambridge International AS & A Level Mathematics : Mechanics Course Book>Chapter 5 - Connected Particles>EXERCISE 5B>Q 2

A bucket of mass 3 kg rests on scaffolding at the top of a building. The scaffolding is 22.5 m above the ground. The bucket is attached to a rope that passes over a smooth pulley. At the other end of the rope there is another bucket of mass 3 kg, which initially rests on the ground. The bucket at the top of the building is filled with 0.6 kg of bricks and is gently released. As this bucket descends, the other bucket rises.

Find how long it will take the descending bucket to reach the ground.