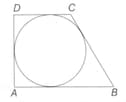
A trapezium inscribes a circle that touches all its sides and the line connecting the mid-points of the non-parallel sides of the trapezium divides the trapezium in such a way that the area of one part is half the area of the other part. If the lengths of the non-parallel sides be $8 \mathrm{cm}$ and $16 \mathrm{cm}$, find the length of the shortest side of the trapezium.

Which of the following is correct, considering the given figure, in which $\mathrm{P}, \mathrm{Q}, \mathrm{R}$ and $\mathrm{S}$ are the mid-points of $\mathrm{AB}, \mathrm{BC}, \mathrm{CD}$ and $\mathrm{AD}$, respectively?

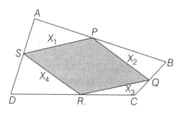
(i) The perimeter of the parallelogram $\mathrm{PQRS}$ is equal to the sum of the diagonals of the quadrilateral $\mathrm{ABCD}$
(ii) ${\mathrm{X}}_1+{\mathrm{X}}_3={\mathrm{X}}_2+{\mathrm{X}}_4$
(iii) $\mathrm{A}\left(\mathrm{PQRS}\right)=\frac{1}{2}\mathrm{A}\left(\mathrm{ABCD}\right)$

In the following quadrilateral $\mathrm{ABCD}, \mathrm{E}$ and $\mathrm{F}$ are the mid-points of $\mathrm{DC}$ and $\mathrm{AB}$, respectively. If the area of $∆\mathrm{ADF}$ is $9{ \mathrm{cm}}^2$ and that of $∆\mathrm{EBC}$ is $18{ \mathrm{cm}}^2$, what is the area of quadrilateral $\mathrm{ABCD}$ ?

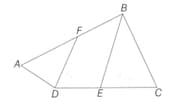
A trapezium $\mathrm{ABCD}$ inscribes a circle. The two sides $\mathrm{AB}$ and $\mathrm{CD}$ are parallel and the diameter of the circle is equal to the length of side $\mathrm{AD} .$ If $\mathrm{DC}=5 \mathrm{cm}$, find the perimeter of the trapezium $\mathrm{ABCD}$.

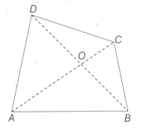
In the following quadrilateral $\mathrm{AC}$ and $\mathrm{BD}$ are the diagonals intersecting at a point $\mathrm{O}$ inside the quadrilateral. The area of $∆\mathrm{AOD}$ is $32{ \mathrm{cm}}^2$ and area of $∆\mathrm{BOC}$ is $18{ \mathrm{cm}}^2$. What is the minimum possible area of the quadrilateral $\mathrm{ABCD} ?$