The position vector r of a particle of mass $m$ is given by, the following equation, r → ( t ) = α t 3 i ^ + β t 2 j ^ m , where α = 10 3 m s - 3 , β = 5 m s - 2 and m = 0 . 1 kg . At, t = 1 s , which of the following statement (s) is are true about the particle?

The torque with respect to the origin is given by, τ → = - 20 3 k ^ Nm .

The force equation is given by, F → = ( i ^ + 2 j ^ ) N

HARD

JEE Main/Advance

IMPORTANT

Earn 100

A uniform circular disc of mass $50 kg$ and radius $0.4 m$ is rotating with an angular velocity of $10 rad s^{- 1}$ about its own axis, which is vertical. Two uniform circular rings, each of mass $6.25 kg$ and radius $0.2 m,$ are gently placed symmetrically on the disc in such a manner that they are touching each other along the axis of the disc and are horizontal. Assume that the friction is large enough such that the rings are at rest relative to the disc and the system rotates about the original axis. The new angular velocity (in $rad s^{- 1}$ ) of the system is

50% studentsanswered this correctly

Important Questions on Rotational Mechanics

HARD

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 10 - Rotational Mechanics>Exercise - 3>Q 25

A uniform wooden stick of mass

1.6 kg

of length

l

rests in an inclined manner on a smooth, vertical wall of height

h (< l)

such that a small portion of the stick extends beyond the wall. The reaction force of the wall on the stick is perpendicular to the stick. The stick makes an angle of

30 °

with the wall and the bottom of the stick is on a rough floor. The reaction of the wall on the stick is equal in magnitude to the reaction of the floor on the stick. The ratio

\frac{h}{l}

and the frictional force

f

at the bottom of the stick are

(g = 10 m s^{- 2})

HARD

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 10 - Rotational Mechanics>Exercise - 3>Q 26

The position vector

r

of a particle of mass $m$ is given by,
the following equation,

\vec{r} (t) = α t^{3} \hat{i} + β t^{2} \hat{j} m

, where

α = \frac{10}{3} m s^{- 3}, β = 5 m s^{- 2}

and

m = 0.1 kg .

At,

t = 1 s,

which of the following statement (s) is are true about the particle?

HARD

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 10 - Rotational Mechanics>Exercise - 3>Q 28

Consider regular polygons with number of sides $n = 3, 4, 5 . . . .$ as shown in the figure. The centre of mass of all the polygons is at height $h$ from the ground. They roll on a horizontal surface about the leading vertex without slipping and sliding as depicted. The maximum increase in height of the locus of the centre of mass for each polygon is $∆$ . Then $∆$ depends on $n$ and $h$ as

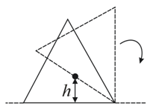
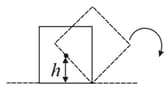
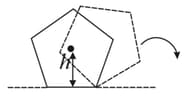
Question Image

MEDIUM

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 10 - Rotational Mechanics>Exercise - 3>Q 29

A wheel of radius $R$ and mass $M$ is placed at the bottom of a fixed step of height $R$ as shown in the figure. A constant force is continuously applied on the surface of the wheel so that it just climbs the step without slipping. Consider the torque $T$ about an axis normal to the plane of the paper passing through the point $Q$ . Which of the following options is/are correct ?

Question Image

HARD

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 10 - Rotational Mechanics>Exercise - 3>Q 32

A ring and a disc are initially at rest, side by side, at the top of an inclined plane which makes an angle

60 °

with the horizontal. They start to roll without slipping at the same instant of time along the shortest path. If the time difference between their reaching the ground is

(\frac{2 - \sqrt{3}}{\sqrt{10}} s)

, then the height of the top of the inclined plane, in metres, is ____. Take

g = 10 {ms}^{- 2} .

HARD

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 10 - Rotational Mechanics>Exercise - 3>Q 33

In the List-I below, four different paths of a particle are given as functions of time. In these functions, $α and β$ are positive constants of appropriate dimensions and $α \neq β$ . In each case, the force acting on the particle is either zero or conservative. In List-II, five physical quantities of the particle are mentioned: p is the linear momentum, L is the angular momentum about the origin, $K$ is the kinetic energy, $U$ is the potential energy and $E$ is the total energy. Match each path in List-I with those quantities in List-II, which are conserved for that path.

Question Image

MEDIUM

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 10 - Rotational Mechanics>Exercise - 3>Q 34

A thin circular ring of mass

m

and radius

R

is rotating about its axis with angular velocity

ω

. Two objects each of mass

M

are attached gently to the opposite ends of a diameter of a ring. The ring rotates with an angular velocity

ω^{'}

given by,

HARD

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 10 - Rotational Mechanics>Exercise - 3>Q 37

A round uniform body of radius

R,

mass

M

and moment of inertia

I

, rolls down (without slipping) an inclined plane making an angle $\theta$ with the horizontal. Then, its acceleration is

Important Questions on Rotational Mechanics

Learn and Prepare for any exam you want !