A rod of length l with thermally insulated lateral surface, consists of a material whose heat conductivity coefficient varies with temperature as k = a T , where a is a constant. The ends of the rod are kept at temperatures T 1 and T 2 . Find the function T x , where x is the distance from the end whose temperature is T 1 .

Consider a rod of length l and area of cross-section A , whose faces are maintained at temperatures θ 1 and θ 2 , respectively. The curved surface of the rod is kept insulated from the surrounding to avoid the leakage of heat. In steady-state, the heat current, i.e., the rate of heat flowing from one face to the other face is given by, d Q d t = k A d T d x Where, k is the coefficient of thermal conductivity of the material of the rod. Let us consider an element of length d x , at a distance x from the hot end, where the temperature drops from T to T - d T . So, d Q d t = - k A d T d x = - a T A d T d x ⇒ d T T = - 1 a A d Q d t d x On integrating, we get, ∫ T 1 T d T T = - 1 a A d Q d t ∫ 0 x d x ⇒ ln T T 1 = - 1 a A d Q d t x ⇒ T = T 1 e - 1 a A d Q d t x Again, T 2 = T 1 e - 1 a A d Q d t l Thus, ln T T 1 ln T 2 T 1 = - 1 a A d Q d t x - 1 a A d Q d t l = x l ⇒ ln T T 1 = x l ln T 2 T 1 ⇒ T T 1 = T 2 T 1 x l ⇒ T = T 1 T 2 T 1 x l

An incandescent bulb has a thin filament of tungsten that is heated to high temperature by passing an electric current. The hot filament emits black-body radiation. The filament is observed to break up at random locations after a sufficiently long time of operation due to non-uniform evaporation of tungsten from the filament. If the bulb is powered at constant voltage, which of the following statement(s) is(are) true?

The filament consumes less electrical power towards the end of the life of the bulb

The temperature distribution over the filament is uniform

The resistance over small sections of the filament decreases with time

HARD

JEE Main/Advance

IMPORTANT

Earn 100

A uniform cylinder of length $L$ and thermal conductivity $k$ is placed on a metal plate of the same area $S$ of mass $m$ and infinite conductivity. The specific heat of the plate is $c$ . The top of the cylinder is maintained at $T_{0}$ . Find the time required for the temperature of the plate to rise from $T_{1}$ to $T_{2} (T_{1} < T_{2} < T_{0})$ .

Important Questions on Heat Transfer

EASY

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 16 - Heat Transfer>Exercise - 4>Q 10

Assume that the total surface area of a human body is

1.6 m^{2}

and that it radiates like an ideal radiator. Calculate the amount of energy radiated per second by the body if the body temperature is

37 ° C

. Stefan constant

σ is 6.0 \times 10^{- 8} W m^{- 2} K^{- 4} . {(31)}^{4} = 923521)

MEDIUM

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 16 - Heat Transfer>Exercise - 4>Q 11

The surface of a household radiator has an emissivity of

0.55

and an area of

1.5 m^{2}

. (a) At what rate is radiation emitted by the radiator when its temperature is

50 ° C

? (b) At what rate is the radiation absorbed by the radiator when the walls of the room are at

22 ° C

? (c) What is the net rate of radiation from the radiator? (Stefan's constant

σ = 6 \times 10^{- 8} W m^{- 2} K^{4}

)

EASY

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 16 - Heat Transfer>Exercise - 4>Q 12

A man, the surface area of whose skin is

2 m^{2}

is sitting in a room where the air temperature is

20 ° C

. If the skin temperature is

28 ° C

, find the net rate at which his body loses heat. [Take the emissivity of skin

0.97

and Stefan’s constant

= 5.67 \times 10^{- 8} W m^{- 2} K^{4}

MEDIUM

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 16 - Heat Transfer>Exercise - 4>Q 13

An electric heater is used in a room of total wall area

137 m^{2}

to maintain a temperature of

+ 20 ° C

inside it, when the outside temperature is

- 10 ° C

. The walls have three different layers of materials. The innermost layer is of wood of thickness

2.5 c m

, the middle layer is of cement of thickness

1.0 c m

and the outermost layer is of brick of thickness

25.0 c m

. Find the power of electric heater. Assume that there is no heat loss through the floor and the ceiling. The thermal conductivities of wood, cement and brick are

0.125, 1.5

and

1.0 W m^{- 1} ° C^{- 1}

, respectively.

HARD

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 16 - Heat Transfer>Exercise - 4>Q 14

A rod of length

l

with thermally insulated lateral surface, consists of a material whose heat conductivity coefficient varies with temperature as

k = \frac{a}{T}

, where

a

is a constant. The ends of the rod are kept at temperatures

T_{1}

and

T_{2}

. Find the function

T (x)

, where

x

is the distance from the end whose temperature is

T_{1}

HARD

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 16 - Heat Transfer>Exercise - 4>Q 15

Two chunks of metal with heat capacities

C_{1}

and

C_{2}

are interconnected by a rod of length

l

and cross-sectional area

S

and fairly low heat conductivity

χ

. The whole system is thermally insulated from the environment. At a moment

t = 0

, the temperature difference between the two chunks of metal equals

Δ T_{0}

. Assuming the heat capacity of the rod to be negligible, find the temperature difference between the chunks, as a function of time.

HARD

JEE Main/Advance

IMPORTANT

Alpha Question Bank for Engineering: Physics>Chapter 16 - Heat Transfer>Exercise - 4>Q 16

It is well known that the temperature of a closed room goes up if the refrigerator is switched on inside it. A refrigerator compartment set to temperature $T_{c}$ is turned on inside a hut in Leh (Ladakh). The atmosphere (outside the hut) can be considered to be a vast reservoir at constant temperature $T_{o}$ . Walls of hut and refrigerator compartment are conducting. The temperature of the refrigerator compartment is maintained at $T_{c}$ with the help of a compressor engine. We explain the working of the refrigerator engine and the heat flow with the help of the associated figure.

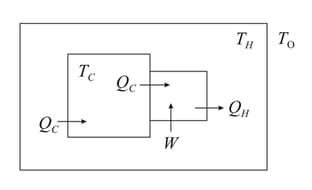
Question Image

The larger square is the refrigerator compartment with heat leak per unit time $Q_{c}$ into it from the room. The same heat per unit time $Q_{c}$ is pumped out of it by the engine (also called compressor and indicated by the smaller square in thick). The compressor does work $W$ and rejects heat per unit time $Q_{H}$ into the hut. The thermal conductance (in units of watt per Kelvin) of the walls of the compartment and hut respectively are $K_{c}$ and $K_{H}$ . After a long time it is found that temperature of the hut is $T_{H}$ . The compressor works as a reverse Carnot engine and it does not participate in heat conduction process.

(a) State the law of heat conduction for the walls of the hut and the refrigerator compartment.

(b) We define the dimensionless quantities $k = \frac{K_{H}}{K_{c}}, h = \frac{T_{H}}{T_{o}}$ and $c = \frac{T_{c}}{T_{o}}$ . Express $h$ in terms of $c$ and $k .$

Important Questions on Heat Transfer

Learn and Prepare for any exam you want !