A uniform rod having mass and length lies on a smooth horizontal surface. A particle of mass moving with speed on the horizontal surface strikes the free rod perpendicularly at an end and it sticks to the rod.
Calculate the velocity of the centre of mass of the system constituting the rod plus the particle.
Calculate the velocity of the particle with respect to before the collision.
Calculate the velocity of the rod with respect to before the collision.
Calculate the angular momentum of the particle and of the rod about the centre of mass before the collision.
Calculate the moment of inertia of the rod plus particle about the vertical axis through the centre of mass after the collision.
Calculate the velocity of the centre of mass and the angular velocity of the system about the centre of mass after the collision.

Important Questions on Centre of Mass, Momentum and Collisions
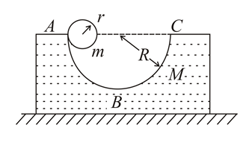
A block of mass with a semicircular track of radius rests on a horizontal frictionless surface. A uniform cylinder of radiusand mass is released from rest from the top point The cylinder slips on the semicircular frictionless track. The distance travelled by the block when the cylinder reaches the point is:
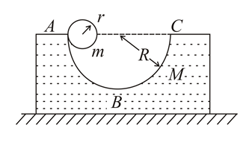
A block of mass with a semicircular track of radius rests on a horizontal frictionless surface. A uniform cylinder of radiusand mass is released from rest from the top point The cylinder slips on the semicircular frictionless track.
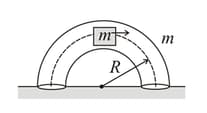
In a vertical plane inside a smooth hollow thin tube a block of same mass as that of tube is released as shown in the figure. When it is slightly disturbed it moves towards right. By the time the block reaches the right end of the tube, displacement of the tube will be (where is mean radius of tube). Assume that the tube remains in vertical plane.
Two men and are standing on a plank. is at the middle of the plank and is at the left end of the plank. The bottom surface of the plank is smooth. The system is initially at rest and masses are as shown in the figure. and start moving such that the position of remains fixed with respect to ground and meets . Then the point where meets is located at
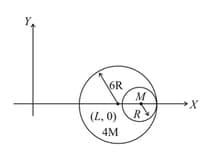
A small sphere of radius is held against the inner surface of a larger sphere of radius . The masses of large and small spheres are respectively. This arrangement is placed on a horizontal table as shown. There is no friction between any surfaces of contact. The small sphere is now released. The coordinates of the centre of the large sphere when the smaller sphere reaches the other extreme position is :