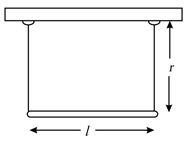
A uniform rod of mass $M$ and length $l$ is suspended by two vertical inextensible strings as shown in figure. Calculate tension in left string at the instant, when right string snaps.

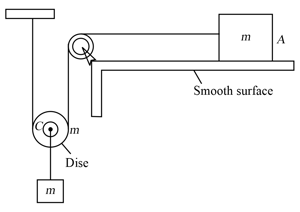
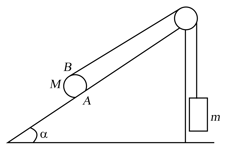
In the figure $A$ and $B$ are identical blocks, each of mass $m$ and $C$ is a circular disc of equal mass $m$. Pulley is massless and ffictionless and thread is inextensible. Neglecting friction, find the acceleration of block $A$ and $B$.

A light thread has been tightly wrapped around a disc of mass $M$ and radius $R$. The disc has been placed on a smooth table, lying flat as shown. The other end of the string has been attached to a mass $m$ as shown. The system is released from rest. Find the acceleration of the disc and block.

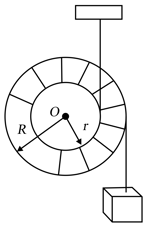
In the arrangement shown, the double pulley has a mass $M$ and the two massless threads have been tightly wound on the inner (radius $=r$) and outer circumference (radius $R=2r$). The block shown has a mass $4M$ . The moment of inertia of the double pulley system about a horizontal axis passing through its centre and perpendicular to the plane of the figure is $I=\frac{M{r}^2}{2}$ . Find acceleration of the center of the pulley after the system is released.
​​​​​​​

A uniform rod of mass $m$ and length $l$ which can rotate freely in vertical plane without friction, is hinged at its lower end on a table. A sphere of mass $m$ and radius $R=l/3$ is placed in contact with the vertical rod and a horizontal force $F$ is applied at the upper end of the rod.

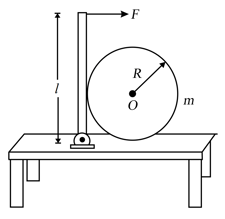
(a) Find the acceleration of the sphere just after the force starts acting.
(b) Find the horizontal component of hinge reaction acting on the rod just after force $F$ starts acting.

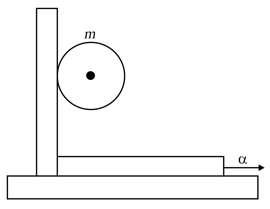
A cylinder of mass $m$ and radius $R$ rolls on a stationary plank of mass $M$ . The lower surface of the plank is smooth and the upper surface is sufficiently rough with a coefficient of friction $\mu$ . A man is to hold the plank stationary with respect to the ground, as shown figure.

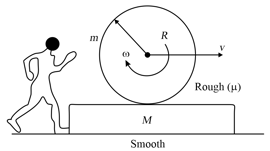
Find the force exerted by the man to keep the plank stationary.

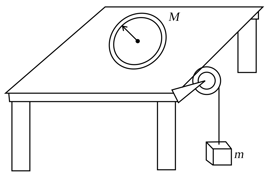
A load of mass $m$ is attached to the end of a string wound on a cylinder of mass $M$ and radius $R$. The string passes round a pulley.

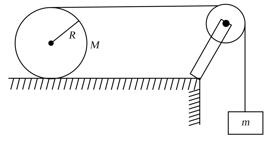
(a) Find the acceleration of the cylinder $M$ when it rolls.
(b) If the coefficient of friction is $\mu$ . Find the acceleration of the cylinder when it slips and rolls.
(c) Find the minimum value of coefficient of friction for which the cylinder rolls always.

Find the tension in the tape and the linear acceleration of the cylinder up the incline, assuming there is no slipping. (Take $M=4m$ and $g=10 \mathrm{m} {\mathrm{s}}^{-2}$ )

A uniform solid sphere rolls down a vertical surface without sliding. If the vertical surface moves with an acceleration $a=\frac{g}{2}$, find the minimum coefficient of friction between the sphere and vertical surfaces so as to prevent relative sliding.