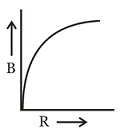
A uniformly charged non-conducting disc of radius having surface charge density . The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular velocity . As a result of this rotation, a magnetic field of induction is obtained at the centre of the disc. If we keep both the charge density of the disc and its angular velocity to be constant and vary the radius of the disc, then the variation of the magnetic induction at the centre of the disc will be represented by the figure.
Important Questions on Moving Charges and Magnetism
The ratio of the magnetic field at the centre of a current-carrying circular coil to magnetic moment is . If the current and the radius both are doubled. The new ratio will become
The rectangular coil of area is in a field Find the torque about the -axis when the coil lies in the position shown and carries a current
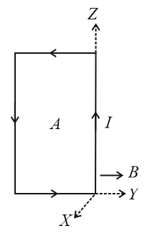
A coil of turns carrying a current of in a magnetic field of . The torque acting on the coil is
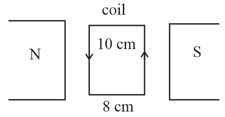
A turns coil shown in figure carries a current of in a magnetic field The torque acting on the coil is
Assume charge of electron, mass of electron and orbital angular momentum of electron
The rectangular loop of dimensions shown in the figure consists of closely wrapped turns and is hinged along the -axis. The plane of the loop makes an angle of with the -axis. The current in the windings is .
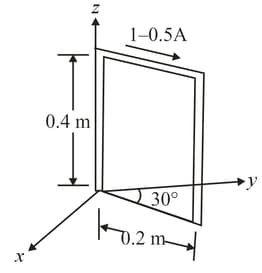
The torque exerted on the loop in this position by a magnetic field
A rectangular loop of sides and , carrying a current of , is placed in different orientations as shown in the figure below.
(a) 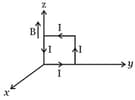 (b)
(b) 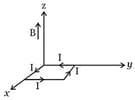
(c) 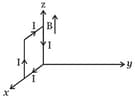 (d)
(d) 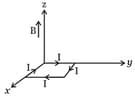
If there is a uniform magnetic field of in the positive direction, in which orientations the loop would be in stable equilibrium and unstable equilibrium?

