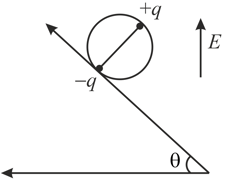
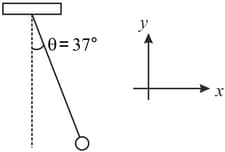
A wheel having mass $\mu$ has charges $+q$ and $-q$ on diametrically opposite points. It remains in equilibrium on a rough inclined plane in the presence of uniform vertical electric field $E$, 

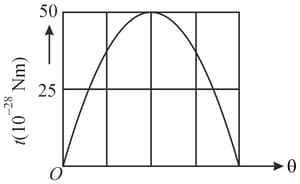
An electric dipole is placed in a uniform electric field $\overrightarrow{E}$ of magnitude $40 \mathrm{N} {\mathrm{C}}^{-1}$. The graph shows the magnitude of the torque on the dipole versus the angle $\mathrm{\theta }$ between the field $\overrightarrow{E}$ and the dipole moment $\overrightarrow{p}$. The magnitude of dipole moment $\overrightarrow{p}$ is equal to

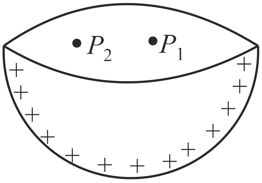
Consider a uniformly charged hemispherical shell shown in the figure. Indicate the directions (not magnitude) of the electric field at the central point $P_1$ and an off-centre point $P_2$ on the drum–head of the shell.

A charged ball of mass $9 \mathrm{k}\mathrm{g}$ is suspended from a string in a uniform electric field $\overrightarrow{\mathit{E}}=\left(3\hat{\mathrm{i}}+5\hat{\mathrm{j}}\right)\times {10}^{5 }\mathrm{N} {\mathrm{C}}^{-1}$. The ball is in equilibrium with $\mathrm{\theta }=37°$. If direction of electric field is reversed, find the new equilibrium position of the ball. Give your answer in terms of angle made by string with vertical. Take, $g=10 \mathrm{m} {\mathrm{s}}^{-1}$.

Given are four arrangements of three fixed electric charges. In each arrangement, a point labelled $P$ is also identified. A test charge $+q$ is placed at $P$. All the charges are of the same magnitude $Q$, but they can be either positive or negative as indicated. The charges and point $P$ all lie on a straight line. The distances between adjacent items, either between two charges or between a charge and point $P$, are all the same.

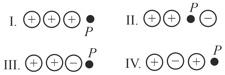
The correct order of choices in decreasing order of magnitude of the force on the $P$ is

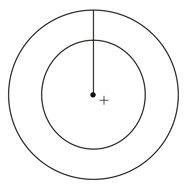
An electrically isolated hollow (initially uncharged) conducting sphere has a small positively charged ball suspended by an insulating rod from its inside surface (see figure).
This causes the inner surface of the sphere to become negatively charged. When the ball is centered in the sphere the electric field outside the conducting sphere is

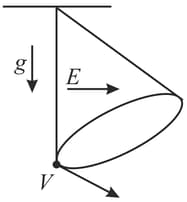
A positively charged particle of charge $q$ and mass $m$ is suspended from a point by a string of length $l$. In the space, a uniform horizontal electric field $E$ exists. The particle is drawn aside so that the string becomes vertical and then it is projected horizontally with velocity $v$ such that the particle starts to move along a circle with same constant speed $v$. Find the speed $v$.