A wheel of rotational inertia $0.100 \mathrm{kg} {\mathrm{m}}^2$ is rotating about a shaft at an angular speed of $160 \mathrm{rev}/\min$. A second wheel is set into rotation at $300 \mathrm{rev}/\min$ and mounted on the same shaft, so that the wheels couple together. Their final angular speed is $200 \mathrm{rev}/\min$. Find (a) the rotational inertia of the second wheel and (b) the change in the rotational kinetic energy of the system due to the rubbing of wheel on wheel.

The figure shows the overhead view of a rod with length, $2L$ and negligible mass which lies on a frictionless surface. Two bullets, each of mass, $m$ and speed, $v$, traveling parallel to the $x$-axis, hit the ends of the rod simultaneously and are buried in the rod. After the collision, what is (a) the angular speed of the system and (b) the speed of the system's center of mass? (c) What is the change in the total kinetic energy because of the collisions?

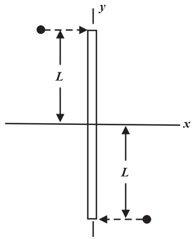
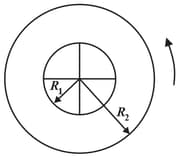
Figure shows an overhead view of a ring that can rotate about its centre like a merry-ground. Its outer radius $R_2$ is $0.800 \mathrm{m}$, inner radius $R_1$ is $R_2/2.00$, mass $M$ is $6.00 \mathrm{kg}$ and the mass of the crossbars at its centre is negligible. It initially rotates at an angular speed of $8.00 \mathrm{rad}/\mathrm{s}$ with a cat of mass $m=M/4.00$ on its outer edge at radius $R_2$. By how much does the cat increase the kinetic energy of the cat-ring system if the cat crawls to the inner edge at radius $R_1$?

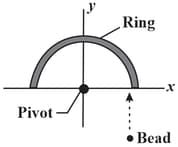
Given figure is an overhead view of semicircular ring of mass $m$, and radius $R$ that lies on a frictionless surface. The ring is connected by elevated spokes (not shown) to a pivot at the centre of the semicircle. The ring can rotate around that pivot but is initially stationary. A bead of mass $m$, and speed $v$ is shot into the ring, entering under the spokes and tangentially to the ring and then sliding along the ring. The ring and bead then rotate together around the pivot. Find their angular speed.

In a long jump, an athlete leaves the ground with an initial angular momentum that tends to rotate her body forward, threatening to ruin her landing. To counter this tendency, she rotates her outstretched arms to "take up" the angular momentum. In $0.700 \mathrm{s}$, one arm sweeps through $0.500 \mathrm{rev}$ and the other arm sweeps through $1.000 \mathrm{rev}$. Treat each arm as a thin rod of mass $4.0 \mathrm{kg}$ and length $0.60 \mathrm{m}$ rotating around one end. In the athlete's reference frame, what is the magnitude of the total angular momentum of the arms around the common rotation axis through the shoulders?

A uniform disk of mass $10m$ and radius $3.0r$ can rotate freely about its fixed centre like a merry-go-round. A smaller uniform disk of mass $m$ and radius $r$ lies on top of the larger disk, concentric with it. Initially, the two disks rotate together with an angular velocity of $20 \mathrm{rad} {\mathrm{s}}^{-1}$. Then a slight disturbance causes the smaller disk to slide outward across the larger disk until the outer edge of the smaller disk catches on the outer edge of the larger disk. Afterwards, the two disks again rotate together (without further sliding).

(a) What then is their angular velocity about the centre of the larger disk?

(b) What is the ratio $\frac{K}{K_0}$ of the new kinetic energy of the two-disk system to the system's initial kinetic energy?

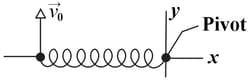
Figure is the overhead view of a spring lying on a frictionless surface and attached to a pivot at its right end. The spring has a relaxed length of  $l_0=1.00 \mathrm{m}$ and negligible mass. A small $0.100 \mathrm{kg}$ disk is attached to the free end at the left. The disk is then given a velocity ${\overrightarrow{v}}_0$ of magnitude $11.0 \mathrm{m} {\mathrm{s}}^{-1}$ perpendicular to the spring's length. The disk and spring then move around the pivot.

(a) When the stretching of the spring reaches its maximum value of  $0.100l_0$, what is the speed of the disk?

(b) What is the spring constant?