HARD
9th ICSE
IMPORTANT
Earn 100
is a kite having and . Prove that the figure formed by joining the midpoints of the sides, in order, is a rectangle.

Important Questions on Mid-Point and Intercept Theorems
HARD
9th ICSE
IMPORTANT
HARD
9th ICSE
IMPORTANT
MEDIUM
9th ICSE
IMPORTANT
HARD
9th ICSE
IMPORTANT
HARD
9th ICSE
IMPORTANT
HARD
9th ICSE
IMPORTANT
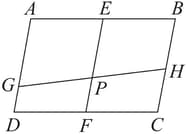
is a parallelogram, is the midpoint of and is the midpoint of . is any line that intersects and in and respectively. Prove that .
HARD
9th ICSE
IMPORTANT
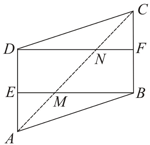
Prove that in a parallelogram, the lines joining a pair of opposite vertices to the mid-points of a pair of opposite sides trisect a diagonal.
MEDIUM
9th ICSE
IMPORTANT
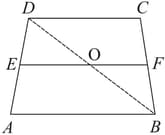
In the figure given below, is the midpoint of side of a trapezium with A line through parallel to , meets in . Show that is the midpoint of .