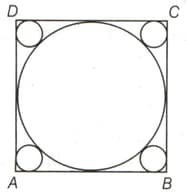
$\mathrm{ABCD}$ is a square, in which a circle is inscribed touching all the sides of a square. In the four corners of square $4$ smaller circles of equal radii are drawn, containing the maximum possible area. What is the ratio of the area of larger circle to that of sum of the areas of four smaller circles?

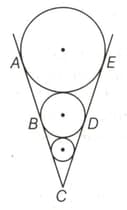
In the adjoining figure $\angle \mathrm{ACE}$ is a right angle. There are three circles which just touch each other where $\mathrm{AC}$ and $\mathrm{EC}$ are the tangents to all the three circles. What is the ratio of radii of the largest circle to that of the smallest circle?

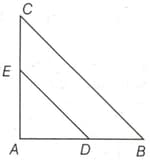
In a right angle triangle $\mathrm{ABC}, \angle \mathrm{A}$ is right angle, $\mathrm{DE}$ is parallel to the hypotenuse $\mathrm{BC}$ and the length of $\mathrm{DE}$ is $65\%$ the length of $\mathrm{BC},$ what is the area of $∆\mathrm{ADE},$ if the area of $∆\mathrm{ABC}$ is $68{ \mathrm{cm}}^2 ?$

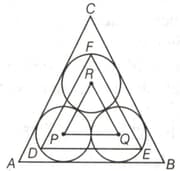
In the adjoining figure three congruent circles are touching each other. Triangle $\mathrm{ABC}$ circumscribes all the three circles. Triangle $\mathrm{PQR}$ is formed by joining the centres of the circle. There is a third triangle $\mathrm{DEF}.$. Points $\mathrm{A}, \mathrm{D}, \mathrm{P}$ and $\mathrm{B}, \mathrm{E}, \mathrm{Q}$ and $\mathrm{C}, \mathrm{F}, \mathrm{R}$ lie in the same straight lines respectively.

What is the ratio of perimeters of $∆\mathrm{ABC}:∆\mathrm{DEF}:∆\mathrm{PQR} ?$

A trapezium $\mathrm{PQRS}$ inscribes a circle which touches the circle at $\mathrm{M}, \mathrm{A}, \mathrm{N}$ and $\mathrm{B}.$ Radius of circle is $10 \mathrm{cm}.$ The length of each non-parallel side is $21 \mathrm{cm}.$ What is the perimeter of the trapezium?

In the given diagram, river $\mathrm{PQ}$ is just perpendicular to the national highway $\mathrm{AB}.$ At a point $\mathrm{B}$ highway just turns at right angle and reaches to $\mathrm{C}. \mathrm{PA}=500 \mathrm{m}$ and $\mathrm{BQ}=700 \mathrm{m}$ and width of the uniformly wide river (i.e., $\mathrm{PQ})$ is $300 \mathrm{m}.$ Also $\mathrm{BC}=3600 \mathrm{m}.$ A bridge has to be constructed across the river perpendicular to its stream in such a way that a person can reach from $\mathrm{A}$ to $\mathrm{C}$ via bridge covering least possible distance. What is the minimum possible required distance from $\mathrm{A}$ to $\mathrm{C}$ including the length of the bridge?

The top of the two parallel towers $\mathrm{AB}$ and $\mathrm{CD}$ can be accessed through two ladders $\mathrm{BC}=210 \mathrm{m}$ and $\mathrm{AD}=174 \mathrm{m}$ such that the foot of each ladder touches the foot of the other building. If there is a tree $\mathrm{EF}=70 \mathrm{m}$ somewhere between the points $\mathrm{A}$ and $\mathrm{C},$ such that the peak of the tree $\mathrm{F}$ is the point of cross section of the two ladders, wherein points $\mathrm{A}, \mathrm{E}$ and $\mathrm{C}$ are collinear, find the horizontal distance $\mathrm{AC}$ between the two towers.

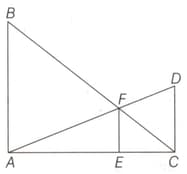
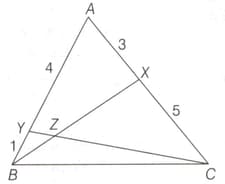
In the following triangle $∆\mathrm{ABC}, \mathrm{AY}: \mathrm{BY}=4: 1$ and $\mathrm{AX}: \mathrm{CX}=3: 5,$ where $\mathrm{X}$ lies on $\mathrm{AC}$ and $\mathrm{Y}$ lies on $\mathrm{AB}$ and $\mathrm{Z}$ is the point of intersection of $\mathrm{BX}$ and $\mathrm{CY}.$ Find the value of $\mathrm{BZ}: \mathrm{CZ}.$