Amul conducted a survey he cheek locking of ice cream flowered among vanilla, chocolate, strawberry for $350$ Per so people like all $3$Ice cream flavours, same no of people like, chocolate &strawberry. The people who like vanilla & chocolate is $60$ & People who like strawberry & vanilla is$40 of 90$ people like vanilla flavour. If $60$ people do not like any flavour & people who like only chocolate is equal to who like only strawberry .

What is the no of people who like only chocolate flavour. 

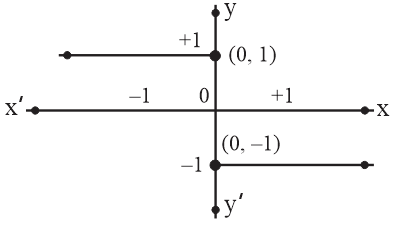
The equation of the graph shown here is:

The solution of linear in equalities $x+y\ge 5$ and $x-y\le 3$ lies:

In the given figure, $AP$ bisect $\angle BAC$. If $\mathrm{AB}=4\mathrm{cm}, \mathrm{AC}=6 \mathrm{cm}$and $\mathrm{BP}=3 \mathrm{cm}$, then the length of $\mathrm{CP}$ is:

Find the ratio in which line $3x+2y=17$ divides the line segment joined by points $\left(2,5\right)$ and $\left(5,2\right).$

If $A(0,-1), B(2,1)$ and $C(0,3)$ are the vertices of $△ABC$, then the length of median drawn from $A$ will be

Find the area of the triangle formed with the three straight lines represented by:

$$\begin{gathered} \left(i\right) x+y=0 \\ \left(ii\right) 3x = 5y; and \\ \left(iii\right) y=3x-12 \end{gathered}$$