An $\alpha$-particle emitted in the radioactive decay of radium has a kinetic energy of $8.0\times {10}^{-13}J$. Calculate the potential difference that an $\alpha$-particle, initially at rest, would have to be accelerated through to gain this energy.

An $\alpha$-particle emitted in the radioactive decay of radium has a kinetic energy of $8.0\times {10}^{-13}J$. Calculate the speed of the a-particle at this kinetic energy.

An $\alpha$-particle emitted in the radioactive decay of radium has a kinetic energy of $8.0\times {10}^{-13}J$.

(b) This diagram shows the path of an $\alpha$-particle of this energy as it approaches a gold nucleus head-on.

(i) State the speed of the $\alpha$-particle at its point of closest approach to the gold nucleus.

An $\alpha$-particle emitted in the radioactive decay of radium has a kinetic energy of $8.0\times {10}^{-13}J$.

(b) This diagram shows the path of an $\alpha$-particle of this energy as it approaches a gold nucleus head-on.

(ii) Write down the kinetic energy of the $\alpha$-particle at this point.

An $\alpha$-particle emitted in the radioactive decay of radium has a kinetic energy of $8.0\times {10}^{-13}J$.

(b) This diagram shows the path of an $\alpha$-particle of this energy as it approaches a gold nucleus head-on.

(iii) Write down the potential energy of the $\alpha$-particle at this point.

An $\alpha$-particle emitted in the radioactive decay of radium has a kinetic energy of $8.0\times {10}^{-13}J$. Show that the $\alpha$-particle will reach a distance of $4.5\times {10}^{-14}\mathrm{m}$ from the centre of the gold nucleus.

An $\alpha$-particle emitted in the radioactive decay of radium has a kinetic energy of $8.0\times {10}^{-13}J$.

(d) Suggest and explain what this information tells us about the gold nucleus.

(Mass of an $\alpha$ -particle $=6.65\times {10}^{-27} \mathrm{kg}$; charge on an $\alpha$ -particle $=+2e$; charge on a gold nucleus $=+79e$.)

This graph shows the electrical potential near an antiproton.

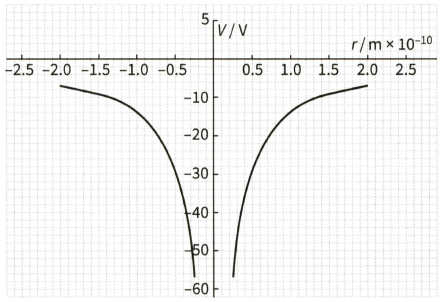
(i) Determine the potential at a distance $.053\times {10}^{-10}m$ from the antiproton.