An electric circuit consists of a current source of emf $\epsilon$ and internal resistance $r$, and two resistors connected in parallel to the source (Fig.). The resistance $R_1$ of one resistor remains unchanged, while the resistance $R_2$ of the other resistor can be chosen so that the power liberated in this resistor is maximum.

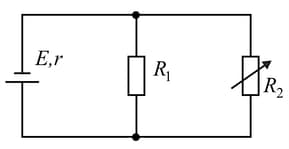
Determine the value of $R_2$ corresponding to the maximum power.

A capacitor of capacitance $C_1$ is discharged through a resistor of resistance $R$.

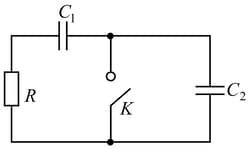
When the discharge current attains the value $I_{0,}$ the key $K$is opened.

Determine the amount of heat $Q$ liberated in the resistor starting from this moment.

Find the amount of heat $Q$ liberated in the resistor after the key $K$ is switched.

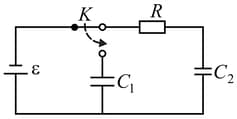
In the circuit diagram shown in Fig. 105 , the capaeitor of capacitanco $C$

is uncharged when the key $K$ is open. The key is closed over some time during which the capacitor becomes charged to a voltage $U$. Determine the amount of heat $Q_2$ liberated during this time in the resistor of resistance $R_2$ if the emf of the source is $E$, and its internal resistance can be neglected.

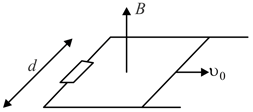
A jumper of mass $m$ can slide without friction along parallel horizontal rails separated by a distance $d$. The rails are connected to a resistor of resistance $R$ and placed in a vertically uniform magnetic field of induction $\overrightarrow{B}$. The jumper is pushed at a velocity $v_0$.

Determine the distance $s$ covered by the jumper before it comes to rest. How does the direction of induction $\overrightarrow{B}$ affect the answer?

A metal ball of radius $r$ moves at a constant velocity $v$ in a uniform magnetic field of induction B.

Indicate the points on the ball the potential difference between which has the maximum value $\Delta {\epsilon }_{\max }$. Find this value, assuming that the direction of velocity forms an angle $\alpha$ with the direction of the magnetic induction.

A direct current flowing through the winding of a long cylindrical solenoid of radius $R$ produces in it a uniform magnetic field of induction $B$. An electron flies into the solenoid along the radius between its turns (at right angles to the solenoid axis)

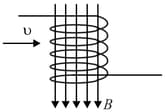
at a velocity $v$ (Fig). After a certain time, the electron deflected by the magnetic field leaves the solenoid.

Determine the time $t$ during which the electron moves in the solenoid.