An electron takes to drift from one end of a metal wire of length to its other end. The area of cross-section of the wire is and it is carrying a current of . The number density of free electrons in the metal wire is
Important Questions on Current Electricity
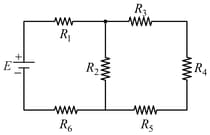
In the figure shown, what is the current (in ampere) drawn from the battery? You are given:
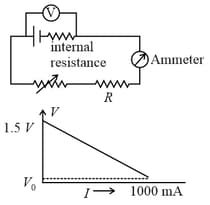
If is almost zero, identify the correct statement:
An ideal ammeter is connected to a battery as shown in the figure. The currents through the resistor and the resistor are, respectively
In the circuit shown below, a student performing Ohm's law experiment accidentally puts the voltmeter and the ammeter as shown in the circuit below; the reading in the voltmeter will be close to
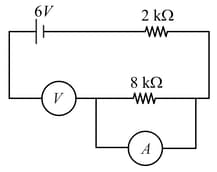
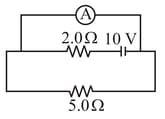
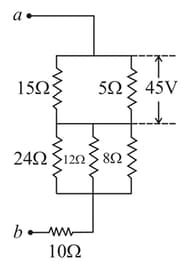
Find the potential difference between and , as shown in the below circuit.
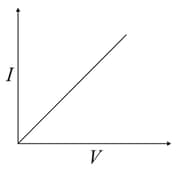
characteristic of a copper wire of length and area of cross-section is shown in figure. The slope of the curve becomes
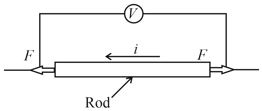
As shown in the schematic below, a rod of uniform cross-sectional area and length is carrying a constant current through it and voltage across the rod is measured using an ideal voltmeter. The rod is stretched by the application of a force .
Which of the following graphs would show the variation in the voltage across the rod as function of the strain when the strain is small. Neglect Joule heating.