The magnetic field at the origin due to a current element i d l → placed at a point with vector position r → is

μ 0 i 4 π r → × d l → r 3

μ 0 i 4 π d l → × r → r 2

μ 0 i 4 π r → × d l → r 2

- μ 0 i 4 π d l → × r → r 4

MEDIUM

Earn 100

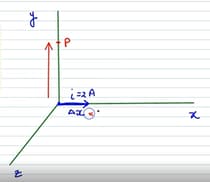
An element $△ l = △ x \hat{i}$ is placed at the origin as shown in figure and carries a current $I = 2 A$ Find out the magnetic field at a point $P$ on the y-axis at a distance of $1.0 m$ due to the element $△ x = 1 cm$ . Give also the direction of the field produced.

Important Questions on Moving Charges and Magnetism

MEDIUM

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

One of the two identical conducting wires of length

L

is bent in the form of a circular loop and the other one into a circular coil of

N

identical turns. If the same current is passed in both, the ratio of the magnetic field at the centre of the loop

(B_{L})

to that at the centre of the coil

(B_{C}),

i.e.

\frac{B_{L}}{B_{C}}

will be

EASY

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

A charged particle going around in a circle can be considered to be a current loop. A particle of a mass

m

carrying charge

q

is moving in a plane with speed

v

under the influence of magnetic field

\vec{B}

. The magnetic moment of this moving particle is :

MEDIUM

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

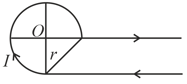
In the given figure, the magnetic field at $' O'$ .

Question Image

HARD

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

The current in flowing along the path $A B C D$ of a cube (shown in the left figure) produces a magnetic field at the centre of cube of magnitude $B$ . Dashed line depicts the non-conducting part of the cube.

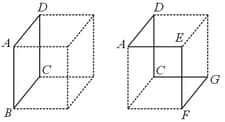
Question Image
Consider a cubical shape shown to the right which is identical in size and shape to the left. If the same current now flows in along the path $D A E F G C D$ , then the magnitude of magnetic field at the centre will be

MEDIUM

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

A cylindrical conductor of radius

R

is carrying a constant current. The plot of the magnitude of the magnetic field

B

with the distance

d

from the centre of the conductor is correctly represented by the figure.

HARD

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

A non-conducting thin disc of radius

R

rotates about its axis with an angular velocity

w

. The surface charge density on the disc varies with the distance

r

from the center as

σ (r) = σ_{0} [1 + {(\frac{r}{R})}^{β}]

, where

σ_{0}

and

β

are constants. If the magnetic induction at the center is

B = (\frac{9}{10}) μ_{0} σ_{0} w R

, the value of

β

EASY

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

An electron revolves in a circular orbit of radius

r

with angular speed

ω

. The magnetic field at the centre of electron orbit is

HARD

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

With the help of Biot-Savart law derive the expression for the intensity of magnetic field at a point due to an infinitely long straight conductor carrying current.

MEDIUM

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

The magnitude of the magnetic field at the centre of an equilateral triangular loop of side

1 m

which is carrying a current of

10 A

is:
[Take

μ_{0} = 4 π \times 10^{- 7} N A^{- 2}

]

EASY

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

A circular coil of wire consisting of

100

turns each of radius

9 cm

carries a current of

0.4 A

. The magnitude of the magnetic field at the centre of coil is

(μ_{0} = 12.56 \times 10^{- 7} SI Units)

MEDIUM

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

Two infinite straight wires

A & B, 1 m

apart are carrying currents of

I

and

4 I

respectively. The distance of the points at which the resultant force is zero is

MEDIUM

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

A point charge

Q = 3 \times 10^{- 12} C

rotates uniformly in a vertical circle of radius

R = 1 mm

. The axis of the circle is aligned along the magnetic axis of the earth. At what value of the angular speed

ω

, the effective magnetic field at the center of the circle will be reduced to zero? (Horizontal component of earth's magnetic field is

30 μ T

)

EASY

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

What is the current in a straight wire. if a magnetic field of

10^{- 6} W m^{- 2}

is produced at a distance of

2 cm

from it?

EASY

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

The magnetic field at the origin due to a current element

i

d \vec{l}

placed at a point with vector position

\vec{r}

MEDIUM

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

Write Biot-Savart's law in vector form.

MEDIUM

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

State and prove Ampere's circuital law.

MEDIUM

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

Write Bio-Savart law in vector form and mentioned the direction of the magnetic field. Which term in the law work as a vector field and produces a magnetic field? Mention one similarity and one dissimilarity between Bio-Savart law for magnetic field and Coulomb’s law for electrostatics.

HARD

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

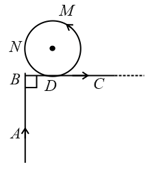
A very long wire ABDMNDC is shown in figure carrying current I. AB and BC parts are straight, long and at right angle. At D wire forms a circular turn DMND of radius R. AB, BC parts are tangential to circular turn at N and D. Magnetic filed at the center of circle is:
Question Image

MEDIUM

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

A small current element of length

d l

and carrying current is placed at (1, 1, 0) and is carrying current in '+ z' direction. If magnetic field at origin be

{\vec{B}}_{1}

and at point (2, 2, 0) be

{\vec{B}}_{2}

then:

MEDIUM

Physics>Electricity and Magnetism>Moving Charges and Magnetism>Magnetic Field due to a Current Element, Biot-Savart Law

A wire bent in the shape of a regular

n

polygonal loop carries a steady current

I

. Let

l

be the perpendicular distance of a given segment and

R

be the distance of a vertex both from the centre of the loop. The magnitude of the magnetic field at the centre of the loop is given by,

An element △l=△xi^ is placed at the origin as shown in figure and carries a current I=2A Find out the magnetic field at a point P on the y-axis at a distance of 1.0 m due to the element △x=1 cm. Give also the direction of the field produced.

Important Questions on Moving Charges and Magnetism

Learn and Prepare for any exam you want !

An element $△ l = △ x \hat{i}$ is placed at the origin as shown in figure and carries a current $I = 2 A$ Find out the magnetic field at a point $P$ on the y-axis at a distance of $1.0 m$ due to the element $△ x = 1 cm$ . Give also the direction of the field produced.