Angular momentum of the particle rotating with a central force is constant due to
Important Questions on Rotational Motion
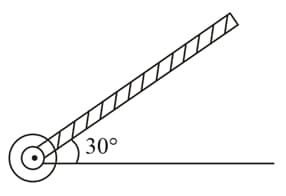
A rod of length is pivoted at one end. It is raised such that it makes an angle of from the horizontal as shown and released from rest. Its angular speed when it passes through the horizontal (in ) will be
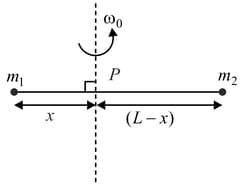
Point masses and are placed at the opposite ends of rigid rod of length , and negligible mass. The rod is to be set rotating about an axis perpendicular to it. The position of point on this rod through which the axis should pass so that the work required to set the rod rotating with angular velocity is minimum, is given by:
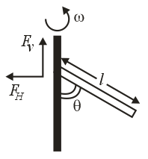
A uniform rod of length ' is pivoted at one of its ends on a vertical shaft of negligible radius. When the shaft rotates at angular speed the rod makes an angle with it (see figure). To find equate the rate of change of angular momentum (direction going into the paper) about the centre of mass (CM) to the torque provided by the horizontal and vertical forces and about the CM. The value of is then such that:
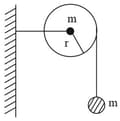
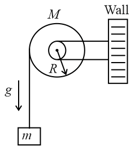
As shown in the figure, a bob of mass is tied to a massless string whose other end portion is wound on a fly wheel (disc) of radius and mass When released from rest the bob starts falling vertically. When it has covered a distance of the angular speed of the wheel will be:
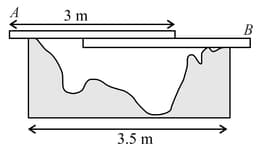
Persons and are standing on the opposite sides of a wide water stream that they wish to cross. Each one of them has a rigid wooden plank whose mass can be neglected. However, each plank is only slightly longer than, So, they decide to arrange them together as shown in the figure schematically. With (the mass ) standing, the maximum mass of , who can walk over the plank is close to,