Answer the following:

An astronaut inside a small spaceship orbiting around the earth cannot detect gravity. If the space station orbiting around the earth has a large size, can he hope to detect gravity?

Important Points to Remember in Chapter -1 - Gravitation from NCERT PHYSICS PART 1 TEXTBOOK FOR CLASS XI Solutions

1. Newton's law of gravitation:

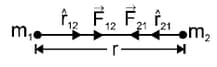
(i) Gravitational force acting between to bodies, $F \propto \frac{m_{1} m_{2}}{r^{2}} or F = G \frac{m_{1} m_{2}}{r^{2}}$ where $G = 6.67 \times 10^{11} N m^{2} {kg}^{2}$ is the universal gravitational constant.

(ii) In vector form: ${\vec{F}}_{12} = \frac{G m_{1} m_{2}}{r^{2}} {\hat{r}}_{12}$ & ${\vec{F}}_{21} = \frac{G m_{1} m_{2}}{r^{2}} {\hat{r}}_{21}$

Question Image

2. Gravitational field:

(i) Gravitational field is related to the force as, $\vec{E} = \frac{\vec{F}}{m}$

(ii) The field produced by a point mass is given by, $\vec{E} = \frac{G M}{r^{2}} \hat{r}$

3. Variation of Acceleration due to Gravity:

(i) Acceleration due to gravity at height $h$ from the surface $g_{h} = \frac{G M_{e}}{{(R_{e} + h)}^{2}} ≃ g (1 - \frac{2 h}{R_{e}})$

(ii) Acceleration due to gravity at depth $d$ from the surface, $g_{d} = g (1 - \frac{d}{R_{e}})$

(iii) The equatorial radius is about $21 km$ longer than its polar radius. Hence $g_{pole} > g_{equator}$

(iv) Acceleration due to gravity at latitude $θ$ , $g' = g - R ω^{2} \cos^{2} θ$

4. Escape velocity:

It is the speed required from the surface of a planet to get out of the influence of the planet. For earth, $v_{e} = \sqrt{\frac{2 G M_{e}}{R_{e}}} = \sqrt{2 g R_{e}}$

5. Satellite in a circular orbit:

(i) Satellite orbital Velocity, $v_{0} = {(\frac{G M_{e}}{R_{e} + h})}^{\frac{1}{2}}$

(ii) Time period of satellite, $T = \frac{2 π {(R_{e} + h)}^{\frac{3}{2}}}{\sqrt{G M_{e}}}$

(iii) Potential energy of a Satellite: $P . E . = \frac{- G M_{e} m}{(R_{e} + h)}$ , Kinetic energy: $K . E . = \frac{G M_{e} m}{2 (R_{e} + h)}$ and total energy $E = - \frac{G M_{e} m}{2 (R_{e} + h)}$

6. Kepler’s Laws:

(i) All planets move in elliptical orbits with the Sun at one of the focal points

(ii) The line joining the sun and a planet sweeps out equal areas in equal intervals of time.

(iii) The square of the orbital period of a planet is proportional to the cube of the semi-major axis of the elliptical orbit of the planet. The time period $T$ and radius $R$ of the circular orbit of a planet about the sun are related as $T^{2} = (\frac{4 π^{2}}{G M_{s}}) R^{3}$