Answer the question based on the given information.

The total cost of snowden ice cream parlour is divided into fixed cost $\left(x\right)$ and variable cost $\left(y\right).$ Fixed cost is the cost that the ice cream parlour has to incur even at zero level of production and variable cost is the cost that will be directly proportional to each unit of ice cream sold.

The parlour launched a new flavour of ice cream and wanted to find the fixed and variable cost associated with it. They found that their total cost for that flavour was Rs $27500$ after selling $150$ units and Rs $32500$ after selling $250$ units.

Find the fixed cost incurred by the ice cream parlour for the new flavour. Show your work.

Ananya had red, blue and yellow marbles in the ratio $4:5:3.$ She gave all her red marbles and some blue marbles to Neha. The ratio of the number of blue marbles and yellow marbles left with Ananya was $7:9.$

If Ananya gave $20$ marbles to Neha, how many of them are red marbles$?$ Show your work.

Is the pair of linear equations $x=p$ and $y=q$ consistent$?$ Justify your answer.

Note: $p$ and $q$ are constants.

Match the graphical representation in column $\mathrm{I}$ with their corresponding criteria in column $\mathrm{II}$ and consequences in column $\mathrm{III}.$

​​​​​​​

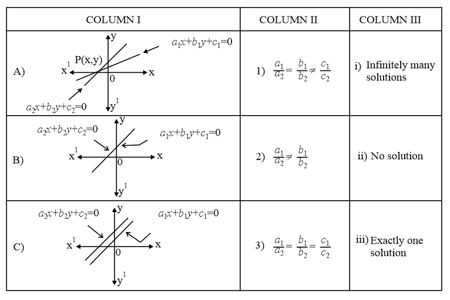
(Note: Match the alphabets $A), B), C)$ in column $\mathrm{I}$ with the corresponding numbers $1)$, $2)$,$3)$ in column $\mathrm{II}$ and $\mathrm{i})$, $\mathrm{ii}),\mathrm{iii})$ in column $\mathrm{iii})$ respectively.

At the Bengaluru marathon, the $42$ km route is designed such that marathoners run in a straight line for $21$ km, and return back along the same path in opposite direction. 

A marathoner, running against the wind, covered the first half of the marathon in $2$ hrs. Then, he covered the second half, running with the wind, in $1.5$ hours. Assume that the marathoner ran at a constant speed and that the wind speed and direction did not change throughout the marathon.

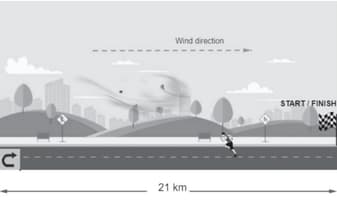
Calculate the speed (in km/h) of the marathoner and the wind. Show your steps. 

A company has a locker in which valuable documents are kept. The passcode is a four digit number of the form $xyyx.$ The Chief Executive Officer (CEO) and the Vice President (VP) of the company have each been given one clue. On solving BOTH clues, the passcode that opens the locker can be found.

CEO's clue: When twice the ones digit is subtracted from the tens digit, the result is $1.$

VP's clue: Three more than the tens digit is thrice the ones digit.

Find the passcode that opens the locker. Show your work.

Shown below are lines $l_1:2x-5y-27=0$ and $l_2:7x-2y+14=0.$

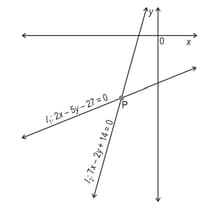
Write the equation of a line $l_{3,}$ in two variables, such that it intersects $l_1$ and $l_2$ exactly at one point., $P.$ Show your work.

Two linear equations in variables $x$ and $y$ are given below.

$a_{1}x+b_{1}y+c=0$

$a_{2}x+b_{2}y+c=0$

Which of the following pieces of information is independently sufficient to determine if a solution exists or not for this pair of linear equations?

I. $\frac{a_1}{b_1}=\frac{a_2}{b_2}=1$ II. $\frac{a_1}{a_2}=\frac{b_1}{b_2}$ III. $\frac{a_1}{a_2}=\frac{a_1}{b_1}\ne 1$ IV. $\frac{a_1}{a_2}\ne \frac{b_1}{b_2}$

Harsh correctly solved a pair of linear equations in two variables and found their only point of intersection as $\left(3, -2\right)$. One of the lines was $x-y=5$. Which of the following could have been the other line?

I: $3x-3y=15$

II: $2x-3y=12$

III: $2x-3y=14$