As a parallel-plate capacitor with circular plates $20 \mathrm{cm}$ in diameter is being charged, the current density of the displacement current in the region between the plates is uniform and has a magnitude of $15 \mathrm{A} {\mathrm{m}}^{-2}.$$\left(a\right)$ Calculate the magnitude $B$ of the magnetic field at a distance $r=50 \mathrm{mm}$ from the axis of symmetry of this region. $\left(b\right)$ Calculate $\frac{dE}{dt}$ in this region. 

A silver wire has resistivity $\rho =1.62\times {10}^{-8 }\mathrm{\Omega }·\mathrm{m}$ and a cross-sectional area of $5.00 {\mathrm{mm}}^2$. The current in the wire is uniform and changing at the rate of $2000 \mathrm{A} {\mathrm{s}}^{-1}$ When the current is $54.0 \mathrm{A}$ .

$\left(a\right)$ What is the magnitude of the (uniform) electric field in the wire when the current in the wire is$100 \mathrm{A}$?

$\left(b\right)$ What is the displacement current in the wire at that time?

$\left(c\right)$ What is the ratio of the magnitude of the magnetic field due to the displacement current to that due to the current at a distance $r$ from the wire? 

The circuit in the figure consists of switch $S$, a $12.0 \mathrm{V}$ ideal battery, a $20.0 \mathrm{M\Omega }$ resistor and an air-filled capacitor. The capacitor has parallel circular plates of radius $6.00 \mathrm{cm},$ separated by $3.00 \mathrm{mm}.$ At time $t=0,$ switch $S$ is closed to begin charging the capacitor. The electric field between the plates is uniform. At $t=250 \mu \mathrm{s},$ what is the magnitude of the magnetic field within the capacitor, at a radial distance $3.00 \mathrm{cm}?$ 

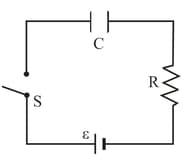
Consider the situation of the previous problem. Define displacement resistance $R_{\mathrm{d}}=\frac{V}{i_{\mathrm{d}}}$ of the space between the plates where $V$ is the potential difference between the plates and $i_{\mathrm{d}}$ is the displacement current. Show that $R_{\mathrm{d}}$ varies with time as $R_{\mathrm{d}}=R\left(e^{\left(\mathrm{t}/\mathrm{\tau }\right)}-1\right)$.

Previous problem: A parallel-plate capacitor having plate-area $A$ and plate separation $d$ is joined to a battery of emf $\epsilon$ and internal resistance $R$ at $t=0$. Consider a plane surface of area $\frac{A}{2}$, parallel to the plates and situated symmetrically between them. Find the displacement current through this surface as a function of time.

A point charge is moving along a straight line with a constant velocity $v$. Consider a small area $A$ perpendicular to the direction of motion of the charge. Calculate the displacement current through the area when its distance from the charge is $x$. The value of $x$ is not large so that the electric field at any instant is essentially given by Coulomb's law