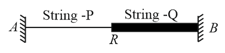
As shown in the figure, two strings $P$ and $Q$ of length $1 \mathrm{m}$ and $\frac{1}{2} \mathrm{m}$ respectively are connected at $A$ and $B$. $R$ is the junction of both strings. A tension of $100 \mathrm{N}$ is maintained in both strings.  The mass per unit length of strings $P$ and $Q$ are $0.16 \mathrm{kg} {\mathrm{m}}^{-1}$ and $0.25 \mathrm{kg} {\mathrm{m}}^{-1}$ respectively. A pulse of amplitude $2 \mathrm{mm}$ is given at point $A$ it partly reflected and partially transmitted at $R$. Then the amplitude of reflected and transmitted wave is:

 

Incident wave $\mathrm{y}=\mathrm{A} \sin \left(\mathrm{ax}+\mathrm{bt}+\frac{\mathrm{\pi }}{2}\right)$ is reflected by an obstacle at $\mathrm{x}=0$ which reduces intensity of reflected wave by $36\%.$ Due to superposition, the resulting wave consists of a standing wave and a travelling wave given by $\mathrm{y}=-1.6 \mathrm{sinax} \mathrm{sinbt}+\mathrm{cA} \cos (\mathrm{bt}+\mathrm{ax})$ where $\mathrm{A}, \mathrm{a}, \mathrm{b}$ and c are positive constants.

Value of $c$ is

Incident wave $\mathrm{y}=\mathrm{A} \sin \left(\mathrm{ax}+\mathrm{bt}+\frac{\mathrm{\pi }}{2}\right)$ is reflected by an obstacle at $\mathrm{x}=0$ which reduces intensity of reflected wave by $36\%.$ Due to superposition, the resulting wave consists of a standing wave and a travelling wave given by $\mathrm{y}=-1.6 \mathrm{sinax} \mathrm{sinbt}+\mathrm{cA} \cos (\mathrm{bt}+\mathrm{ax})$ where $\mathrm{A}, \mathrm{a}, \mathrm{b}$ and c are positive constants.

Amplitude of reflected wave is