EASY
Earn 100
Assertion: Specific heat of gas at constant pressure is greater than its specific heat at constant volume.
Reason: At constant pressure, some heat is spent in expansion of the gas.
(a)If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
(b)If both Assertion and Reason are true but Reason is not correct explanation of the Assertion.
(c)If Assertion is true but the Reason is false.
(d)If Assertion is false but Reason is true.
50% studentsanswered this correctly
Important Questions on Thermodynamics
MEDIUM
MEDIUM
[Given that
HARD
EASY
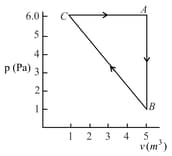
For the given cyclic process as shown for a gas, the work done is:
EASY
EASY
HARD
HARD
EASY
EASY
EASY
MEDIUM
MEDIUM
What will be the molar specific heat at constant volume of an ideal gas consisting of rigid diatomic molecules?
MEDIUM
MEDIUM
MEDIUM
EASY
MEDIUM
EASY
(Take gas constant )
EASY

