EASY

Earn 100

Assertion $(A) :$ Fan spins even after switch is off

Reason $(R) :$ Fan in rotation has rotational inertia

50% studentsanswered this correctly

Important Questions on Rotational Dynamics

MEDIUM

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

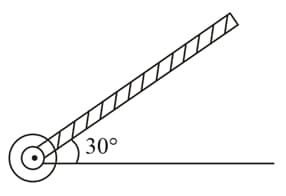
A rod of length $50 c m$ is pivoted at one end. It is raised such that it makes an angle of $30^{o}$ from the horizontal as shown and released from rest. Its angular speed when it passes through the horizontal (in $r a d s^{- 1}$ ) will be $(g = 10 m s^{- 2})$

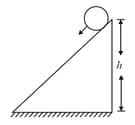
Question Image

HARD

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A uniformly thick wheel with moment of inertia

I

and radius

R

is free to rotate about its centre of mass (see fig). A massless string is wrapped over its rim and two blocks of masses

m_{1}

and

m_{2} (m_{1} > m_{2})

are attached to the ends of the string. The system is released from rest. The angular speed of the wheel when

m_{1}

descends by a distance

h

is:

MEDIUM

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A solid cylinder of mass $m$ and radius $R$ rolls down inclined plane without slipping. The speed of its $C . M .$ when it reaches the bottom is___

Question Image

MEDIUM

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

Kinetic energy of rotation of a flywheel of radius

2 m,

mass

8 kg

and angular speed

4 rad s^{- 1}

about an axis perpendicular to its plane and passing through its center is

EASY

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

Two discs of same moment of inertia

(I)

are rotating in same sense about their regular axis passing through centre and perpendicular to the plane of disc with angular velocities

ω_{1}

and

ω_{2}

. They are brought into contact face to face coinciding the axis of rotation. The expression for loss in energy during this process is

MEDIUM

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A disc of mass

M

and radius

R

rolls without slipping on a level surface with a linear speed

v

. Its kinetic energy will be given by

MEDIUM

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A wheel is rotating freely with an angular speed

ω

on a shaft. The moment of inertia of the wheel is

I

and the moment of inertia of the shaft is negligible. Another wheel of moment of inertia

3 I

initially at rest is suddenly coupled to the same shaft. The resultant fractional loss in the kinetic energy of the system is:

EASY

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

Two bodies have their moments of inertia

I

and

2 I

respectively about their axes of rotation. If their kinetic energies of rotation are equal, their angular momenta will be in the ratio__

EASY

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A disc of radius

2 m

and mass

100 k g

rolls on a horizontal floor. Its centre of mass has speed of

20 c m s^{- 1} .

How much work is needed to stop it?

MEDIUM

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A solid sphere and solid cylinder of identical radii approach an incline with the same linear velocity (see figure). Both roll without slipping all throughout. The two climb maximum heights $h_{s p h}$ and $h_{c y l}$ on the incline. The ratio $\frac{h_{s p h}}{h_{c y l}}$ is given by:
Question Image

MEDIUM

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A wheel is at rest in horizontal position. Its

M . I .

about vertical axis passing through its centre is

I

. A constant torque

τ

acts on it for

t

second. The change in rotational kinetic energy is

EASY

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A solid sphere of mass

2 kg

is rolling on a frictionless horizontal surface with velocity

6 m s^{- 1}

. It collides on the free end of an ideal spring whose other end is fixed. The maximum compression produced in the spring will be (Force constant of the spring =

36 N m^{- 1}

EASY

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A solid cylinder of mass

M

and radius

R

rolls down a smooth inclined plane about its own axis and reaches the bottom with velocity

v

. The height of the inclined plane is (

g =

acceleration due to gravity)

MEDIUM

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A cylinder of mass

2 kg

is released from rest from the top of an inclined plane of inclination

30 °

and length

1 m

. If the cylinder rolls without slipping, then its speed when it reaches the bottom is [

g = 10 m s^{- 2}

]

HARD

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A wheel of mass

10 kg

and radius

0.8 m

is rolling on a road with an angular speed

20 {rads}^{- 1}

without sliding. The moment of inertia of the wheel about the axis of rotation is

1.2 {kgm}^{2},

then the percentage of rotational kinetic energy in the total kinetic energy of the wheel is ____________(approximately)

MEDIUM

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A uniform circular disc of mass

400 g

and radius

4.0 cm

is rotated about one of its diameter at an angular speed of

10 rad s^{- 1}

. The kinetic energy of the disc is

EASY

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

The ring of radius

1 m

and mass

15 kg

is rotating about its diameter with angular velocity of

25 rad / \sec

. Its kinetic energy is

MEDIUM

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A stationary horizontal disc is free to rotate about its axis. When a torque is applied on it, its kinetic energy as a function of

θ

, where

θ

is the angle by which it has rotated, is given as

k θ^{2}

. If its moment of inertia is

I

then the angular acceleration of the disc is:

HARD

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A uniform thin rod of length

2 L

and mass

m

lies on a horizontal table. A horizontal impulse

J

is given to the rod at one end. There is no friction. The total kinetic energy of the rod just after the impulse will be

EASY

Physics>Mechanics>Rotational Dynamics>Kinetic Energy of a Rotating Body

A solid sphere of mass,

m

and radius,

R

is rotating about its diameter. A solid cylinder of the same mass and same radius is also rotating about its geometrical axis with an angular speed twice that of the sphere. The ratio of their kinetic energies of rotation

(\frac{E_{sphere}}{E_{cylinder}})

will be

Assertion (A): Fan spins even after switch is off Reason (R): Fan in rotation has rotational inertia

Important Questions on Rotational Dynamics

Learn and Prepare for any exam you want !

Assertion $(A) :$ Fan spins even after switch is off

Reason $(R) :$ Fan in rotation has rotational inertia