Assertion $\left(\mathrm{A}\right)$: If ratio of perimeters of two similar triangles is $6:11$, then ratio of their corresponding medians is also $6:11$.

Reason $\left(\mathrm{R}\right)$: Converse of B.P.T. states that if two sides of a triangle are divided by a line in equal ratio then the line is parallel to the third side.

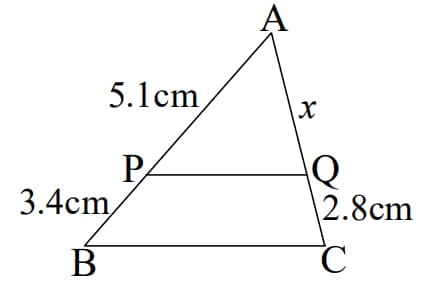
The line parallel to $BC$ of $∆ABC$ meets $AB$ and $AC$ at $P$ and $Q$ respectively. If $AP=4 cm$, $QC=9 cm$ and $PB=AQ$, then find the length of $PB$.

Write the statement of Basic Proportionality Theorem (Thales Theorem).

In the adjoining figure, if $PQ\parallel BC$, Find $x$.

In $△ABC, A-M-B, A-N-C, \overline{MN}\parallel \overline{BC}$. If $AM:AB=2:3$ and $AC=15$, then $NC=$ _____.

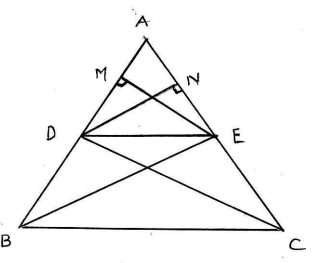
Given : $D$ is any point on side $BC$ of $△ABC$. $\mathrm{DE}\Vert \mathrm{AB}\text{ and }\mathrm{DF}\Vert \mathrm{AC}\text{. }$$A-F-B$ and $A-E-C$. $EF$ and $CB$ meet at $H$ when produced as shown in the fig. Prove that: ${\mathrm{HD}}^2=\mathrm{HB}\times \mathrm{HC}$

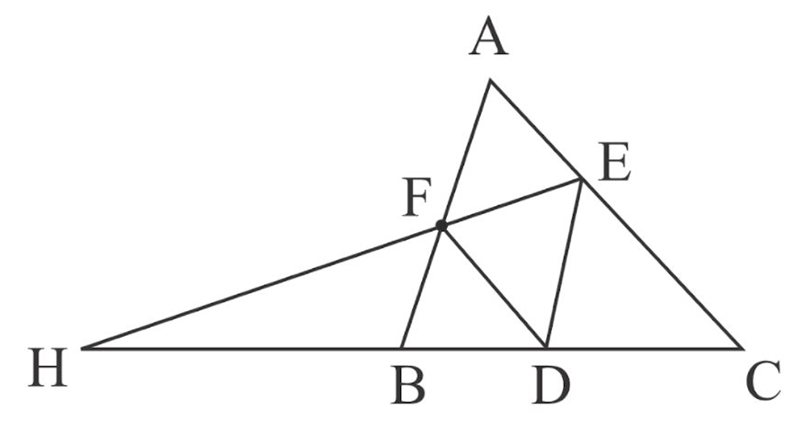
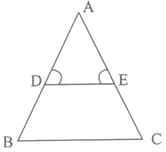
In figure, $\angle D=\angle E$ and $\frac{AD}{DB}=\frac{AE}{EC}$, prove that $BAC$ is an isosceles triangle.

If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio. Prove it.

$ABCD$ is a trapezium in which $AB\parallel DC$ and its diagonal intersect each other at a point $O$. Show that:

$\frac{AO}{BO}=\frac{CO}{OD}$

Given : In $∆\mathrm{ABC},\mathrm{DE}\Vert \mathrm{BC}$ where the points $D$ and $E$ lie on $AB$ and $AC$ respectively, $\mathrm{EM}\perp \mathrm{AB}$ and $\mathrm{DN}\perp \mathrm{AC}:$

Prove that : $\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}$

In the figure, $DE\parallel BC$ and $\frac{AD}{DB}=\frac{2}{3}$. If $EC=6 \mathrm{cm}$, find $AE$.